Functional Programming in Python
Keyword call outs
Implicit and explicit line continuation: Wrap long lines using implied line continuation inside parentheses, brackets, and braces, or use explicit line continuation with the
\character to terminate a line (no space afterwards). Use PEP 8 as a reference.Comments and docstrings: There are no multiline comments in Python. Multiline strings can be used with triple single- or double-quote delimiters:
'''or""". These can also be used for docstrings. See PEP 257 for docstring conventions.Keywords: List of keywords can be found by running
import keyword
print(keyword.kwlist)whileandforloops can haveelseblocks: Whatever code is in theelseclause will be executed if thewhileorforloop never encounters abreakstatement. Hence, if you use anelseclause in awhile/forloop that does not have abreakstatement, then the code within theelseblock will be automatically executed at the end of the loop. The takeaway: theelseclause only fires if the loop terminates properly (i.e., without hitting abreakstatement).finallyalways executes: Thewhileloop starts by always evaluating the conditional expression first, which does not guarantee that your loop will run at least once. If you need to ensure that yourwhileloop runs at least once, then you can use thewhile Trueapproach. Thewhileloop has anelseclause that can be attached which executes if and only if thewhileloop terminates normally (i.e., without encountering abreakstatement). Finally,continueandbreakstatements can be used inside atrystatement inside a loop and thefinallywill always execute before eitherbreaking orcontinueing from that point forward.Iterables: In Python, an iterable is an object capable of returning values one at a time. The
forloop in Python iterates an iterable.
Preliminaries
The Zen of Python and "Idiomatic Python"
To program in "idiomatic Python", we need to embrace the Zen of Python. From PEP 8:
Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one--and preferably only one--obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!
This listing can also be obtained by running import this in the Python interpreter.
Basics (Python refresher)
The Python type hierarchy
The following is a subset of the Python type hierarchy but the subset you will deal with most often.
Numbers
| Integral | Non-Integral |
|---|---|
| Integers | Floats |
| Booleans | Complex |
| Decimals | |
| Fractions |
Collections
| Sequences | Sets | Mappings |
|---|---|---|
| Lists (mutable) | Sets (mutable) | Dictionaries |
| Tuples (immutable) | Frozen Sets (immutable) | |
| Strings (immutable) |
Callables
A callable is anything you can "call" or invoke:
- User-defined functions
- Generators
- Classes
- Instance methods
- Class instances (
__call__()) - Built-in functions (e.g.,
len(),open()) - Built-in methods (e.g.,
my_list.append(x))
Singletons
NoneNotImplemented- Ellipsis (
...)
Multi-line statements and strings
Overview
A Python program is basically nothing more than just a text file that contains physical lines of code. These physical lines of code are often separated by physical newlines that are inserted by you by pressing the Enter key on your keyboard. The physical code is processed by the Python compiler, and it is then combined to produce logical lines of code which are then tokenized so that the Python compiler and interpreter can understand what your code is trying to do and execute it accordingly:
Python program
-> physical lines of code
-> logical lines of code
-> tokenized
-> executed
Physical lines of code end with a physical newline character and once the code has been processed, logical lines of code will end with a logical NEWLINE token. Exactly how this gets done is not really the important part. That's what the Python development team is for!
The important thing for us to understand is that there is a difference between a physical newline character and a logical NEWLINE token. They're not necessarily the same thing. Very often they are but not always. Sometimes physical newlines are ignored and they are ignored in order to combine multiple physical lines into a single logical line of code which is then terminated by a logical newline token. This is what allows us to write code over multiple lines that technically should be written as a single line (kind of like a SQL query). But we want to be able to write code over multiple lines for the sake of readability. It allows us to make our code easier to read and understand. The Python interpreter and compiler really doesn't care whether you write your code over one line, two lines, thousands of lines, etc. At the end of the day, it will recombine lines of code into single lines as needed, it will tokenize everything, etc. It does not care at all about human readability. But we humans should care about readability!
Implicit and explicit conversions
The conversion between physical and logical newlines (i.e., the removal of physical newline characters) is done either implicitly or explicitly. Many times we can get by and let implicit conversions do their thing. But sometimes we have to be explicit.
Implicit examples
The following expressions may be written across multiple physical lines (they also support inline comments):
- list literals:
[] - tuple literals:
() - dictionary literals:
{} - set literals:
{} - function arguments / parameters
So a list like [1,2,3] does not have to be written as a single line. It can be written across several lines (i.e., across physical newlines):
[1,
2,
3]
Of course, it makes little sense in this example to write the list like this, but you can imagine scenarios where maybe you have lists with variables with very long names. Sometimes it might be much clearer to write a list using physical newlines. Those physical newlines will be implicitly removed by Pyhon.
You can also add comments to the end of each physical line (before the physical newline character):
[
1, # first element
2, # second element
3 # third element
]
Although not as pretty or conventional, you can also write the above in the following manner (both approaches are valid):
[
1 # first element
,2 # second element
,3 # third element
]
Note that if you do use comments, however, you must close off the collection on a new line. For example, the following will not work since the closing ] is actually part of the comment:
[1, # first element
2 #second element]
This works the same way for tuples
a = (
1, # first element
2, # second element
3, # third element
)
and sets
a = {
1, # first element
2, # second element
}
and dictionaries
a = {
'key1': 'value1', #comment
'key2': 'value2' #comment
}
We can also break up function arguments and parameters (which can be quite useful for when your function has numerous parameters or the arguments provided have long names);
def my_func(a, # arg1 comment
b, # arg2 comment
c): # arg3 comment
print(a, b, c)
my_func(
10, # param1 comment
20, # param2 comment
30 # param3comment
)
All of the examples above involve implicit conversion of physically multi-line code into logically single-line code (including the implicit stripping of comments and the like).
Explicit examples
The PEP 8 -- Style Guide for Python Code is worth taking a look at. In particular, note what it says about the preferred way of wrapping long lines:
The preferred way of wrapping long lines is by using Python's implied line continuation inside parentheses, brackets and braces. Long lines can be broken over multiple lines by wrapping expressions in parentheses. These should be used in preference to using a backslash for line continuation.
Backslashes may still be appropriate at times. For example, long, multiple
with-statements cannot use implicit continuation, so backslashes are acceptable:
with open('/path/to/some/file/you/want/to/read') as file_1, \
open('/path/to/some/file/being/written', 'w') as file_2:
file_2.write(file_1.read())
As can be seen above, when necessary, you can use the backslash character \ (with no trailing space after the backslash) to explicitly create multi-line statements:
a = 10
b = 20
c = 30
if a > 5 \
and b > 10 \
and c > 20:
print('yes!!')
The identation in explicitly continued lines does not matter:
a = 10
b = 20
c = 30
if a > 5 \
and b > 10 \
and c > 20:
print('yes!!')
The takeaway from all of this is that multi-line statements (i.e., as opposed to expressions within braces or brackets) are not implicitly converted to a single logical line in Python. Something like
if a
and b
and c:
will not work. Python will throw an error. It will place a NEWLINE token after if a, but it will expect a colon.
One workaround for using the multi-line format is to use PEP 8's advice and take advantage of "Python's implied line continuation inside parentheses, brackets and braces":
a = 10
b = 20
c = 30
if (a > 5
and b > 10 # this comment is fine
and c > 20):
print('yes!!')
Or we can be explicit with our multi-line format and use the \ character (note, however, that comments cannot be part of a statement, not even a multi-line statement, so if you use \ then your comments will need to go above where you start using \ characters or below the last occurrence):
# this comment is fine
if a \
and b \ # this comment is NOT fine
and c: # this comment is fine
Multi-line strings
You can create multi-line strings by using triple delimiters (single or double quotes):
>>> a = '''this is
... a multi-line string'''
>>> a
'this is\na multi-line string'
Note how the physical newline we typed in the multi-line string was preserved (i.e., the physical newline character \n is preserved).
The results are somewhat less visible if we run this as part of a script:
a = '''this is
a multi-line string'''
print(a)
this is
a multi-line string
In general, any character you type is preserved. You can also mix in escaped characters like any normal string.
a = """some items:\n
1. item 1
2. item 2"""
print(a)
some items:
1. item 1
2. item 2
Be careful if you indent your multi-line strings. The extra spaces are preserved!
def my_func():
a = '''a multi-line string
that is actually indented in the second line'''
return a
print(my_func())
a multi-line string
that is actually indented in the second line
In such a case, it is appropriate to manually remove what otherwise might look like normal indenting:
def my_func():
a = '''a multi-line string
that is actually not indented in the second line'''
return a
print(my_func())
a multi-line string
that is actually not indented in the second line
Important to note is that these multi-line strings are not comments--they are real strings and, unlike comments, are part of your compiled code. They are, however, sometimes used to create comments, such as docstrings (something that will be covered later). See the article PEP 257 -- Docstring Conventions for more.
In general, use # to comment your code, and use multi-line strings only when actually needed (like for docstrings).
Also, there are no multi-line comments in Python. You simply have to use a # on every line.
# this is
# a multi-line
# comment
The following works, but the above formatting is preferrable:
# this is
# a multi-line
# comment
Variable names
We will mostly look at rules and conventions related to identifier names. We can start with the fact that identifiers are case-sensitive. So the following are all different identifiers:
my_var
my_Var
ham
Ham
Rules
Identifiers must follow certain rules and should follow certain conventions:
Strict rules
start with an underscore (
_) or letter (a-z,A-Z) You can technically go beyond this, but it's wise to stick with this character set.followed by any number of underscores (
_), letters (a-z,A-Z), or digits (0-9)cannot be reserved words. Most of these words you'll already be familiar with (e.g.,
True,False,while, etc.), but you can find the complete list by using thekeywordmodule that is part of the standard library:import keyword
print(keyword.kwlist)This gives us the following list (string quotes removed):
[False, None, True, __peg_parser__, and, as, assert, async, await, break, class, continue, def, del, elif, else, except, finally, for, from, global, if, import, in, is, lambda, nonlocal, not, or, pass, raise, return, try, while, with, yield]All of the following are legal names although the last three conventionally have a special meaning associated with them:
var
my_var
index1
index_1
_var
__var
__lt__
Implied rules (conventions)
_my_var: It is convention to use a single underscore as part of an identifier to indicate "internal use" or "private" objects. This is a way to communicate to anyone looking at or using your code that they really shouldn't mess around with that variable. Worth noting is that objects named this way will not get imported by a statement such as the following:from module import *.__my_var: The double underscore or "dunder" is used for so-called name mangling. This basically changes your variable in a very set way that can be useful for inheritance chains if you have the same name, say attribute or property in a class, and you have the same attribute in a chain of classes, then how do you differentiate which is which? This is where name mangling comes in. When you want name mangling to occur, you use__in front of your variable name (short version:__is used to mangle class attribues which is something useful in inheritance chains).__my_var__: Double underscores that both start and end an identifier name are used for system-defined names that have a special meaning to the interpreter. For example, suppose you have instancesxandyof a class that you have created. If you try to evaluatex < y, then the Python interpreter will automatically look for an__lt__method defined on the class for whichxandyare instances and runx.__lt__(y). Point being: don't invent so-called magic methods (i.e., double underscore methods)! Stick to the ones pre-defined by Python. Which ones exist? The special method names article in the Python language reference is a good place to look. There you can find more information about frequently used dunder methods like__init__and others.- Packages: Short, all-lowercase names. Preferably no underscores. So something like
utilitieswould work well. - Modules: Short, all-lowercase names. Can have underscores. Something like
db_utilsordbutilswould be fine. - Classes: CapWords (upper camel case) convention. So something like
BankAccountwould work fine. - Functions: Lowercase, words separated by underscores (snake_case). So something like
open_accountwould work well. - Variables: Lowercase, words separated by underscores (snake_case). So something like
account_idwould work well. - Constants: All-uppercase, words separated by underscores. So something like
MIN_APRwould work well.
The while loop
Python does not have a do ... while construction like some other langauges have to ensure the while loop fires at least once. But it is easy to mimic:
i = 5
while True:
print(i)
if i >= 5:
break
i += 1
When it comes to prompts especially, you may find yourself doing something not quite DRY:
min_length = 2
name = input("Please enter your name: ")
while not (len(name) >= min_length and name.isprintable() and name.isalpha()):
name = input("Please enter your name: ")
print("Hello, {0}".format(name))
We can clean this up fairly easily:
min_length = 2
while True:
name = input("Please enter your name: ")
if (len(name) >= min_length and name.isprintable() and name.isalpha()):
break
print("Hello, {0}".format(name))
The break statement breaks out of the loop and terminates the loop immediately. The continue statement, however, is a little bit different. It's like saying, "Hey, the current iteration of the loop we're in right now ... I want you to break out of that. Skip everything that comes after this continue statement and go back to the beginning of the loop."
A trivial but illustrative example:
a = 0
while a < 10:
a += 1
if a % 2 == 0:
continue
print(a)
This results in printing off 1, 3, 5, 7, and 9. The continue statement ensures the print statement is never reached for even numbers, but the loop continues to run.
Something interesting about while loops in Python is that you can use an else statement with them. The else clause of the while loop will execute if and only if the while loop did not encounter a break statement; that is, if the loop ran normally, then it will end up executing the code inside the else statement. This can be quite useful.
A simple example might be something like the following:
l = [1, 2, 3]
val = 10
found = False
idx = 0
while idx < len(l):
if l[idx] == val:
found = True
break
idx += 1
if not found:
l.append(val)
print(l)
This looks through the list l and adds the val if it is not found (we could obviously do this in more effective ways but the goal here is to use a while loop). The else statement could be helpful here:
l = [1, 2, 3]
val = 10
idx = 0
while idx < len(l):
if l[idx] == val:
break
idx += 1
else:
l.append(val)
print(l)
The outcome is the same for both of these programs. The takeaway: the else clause for a while loop only fires if the while loop terminates properly (i.e., without hitting a break statement). Hence, something like
i = 1
while i < 10:
print(i)
i += 1
else:
print('Woohoo!')
will have the following output:
1
2
3
4
5
6
7
8
9
Woohoo!
Since there is no possibility of running into a break in the while loop above, the code in the else statement will automatically be executed once the while loop terminates.
break, continue, and try statements
We are now going to look at what happens when you try to use break and continue when you are inside a try statement inside a loop. So the question is: What happens? Recall that for try statements we have try...except...finally, where try is what we are trying to do, except is where we can trap specific exceptions, but there is also a finally clause that exsits that always runs even when there is an exception.
For example:
a = 10
b = 1
try:
a/b
print(a/b)
except ZeroDivisionError:
print('Division by zero')
finally:
print('This always executes.')
Output:
10.0
This always executes.
And if we change b to 0 to have
a = 10
b = 0
try:
a/b
print(a/b)
except ZeroDivisionError:
print('Division by zero')
finally:
print('This always executes.')
then we will get
Division by zero
This always executes.
Now consider the following code block:
a = 0
b = 2
while a < 4:
print('-------------')
a += 1
b -= 1
try:
a/b
except ZeroDivisionError:
print("{0}, {1} - division by 0".format(a,b))
continue
finally:
print('{0}, {1} - always executes'.format(a,b))
print("{0}, {1} - main loop".format(a,b))
We end up with the following output:
-------------
1, 1 - always executes
1, 1 - main loop
-------------
2, 0 - division by 0
2, 0 - always executes
-------------
3, -1 - always executes
3, -1 - main loop
-------------
4, -2 - always executes
4, -2 - main loop
Note how the finally block executes even though we had a continue statement. If we replace continue with break, then the finally block will still execute and then the loop will be broken out of:
a = 0
b = 2
while a < 4:
print('-------------')
a += 1
b -= 1
try:
a/b
except ZeroDivisionError:
print("{0}, {1} - division by 0".format(a,b))
break
finally:
print('{0}, {1} - always executes'.format(a,b))
print("{0}, {1} - main loop".format(a,b))
This gives us
-------------
1, 1 - always executes
1, 1 - main loop
-------------
2, 0 - division by 0
2, 0 - always executes
The upshot of all this is that finally will always run! Exception or not. break or continue or not! We can combine this useful information with the else clause if we want. Recall when else executes: Whenever a while loop terminates normally (i.e., no break clause is encountered).
Recap: The while loop starts by always evaluating the conditional expression first, which does not guarantee that your loop will run at least once. If you need to ensure that your while loop runs at least once, then you can use the while True approach. The while loop has an else clause that can be attached which executes if and only if the while loop terminates normally (i.e., without encountering a break statement). Finally, continue and break statements can be used inside a try statement inside a loop and the finally will always execute before either breaking or continueing from that point forward.
The for loop
The for loop construct in most C-like languages is as follows:
for (int i = 0; i < 5; i++) { ... }
The int i = 0 statement is executed at the beginning of the loop and the condition i < 5 is checked before the loop runs every time, and the last statement declares what happens at the end of each iteration. Python has no such construct!
To understand the for loop construct in Python, we first need to understand what an iterable is:
In Python, an iterable is an object capable of returning values one at a time.
We could construct something similar to the for loop syntax above in Python:
i = 0
while i < 5:
print(i)
i += 1
i = None
The last part is to mimic how i goes out of scope at the end of the for loop in most languages. We really don't need to do this in practice though (everything gets cleaned up for us).
In any case, this is obviously not what we do in Python to use for loops. The for statement in Python is something to iterate over an iterable. A very simple iterable we can create is by using the range function:
for i in range(5):
print(i)
The important takeaway here is that for iterates an iterable in Python. In fact, range is neither a collection nor a list. It is specifically an iterable. Of course, in general, lists, strings, tuples, etc., are iterables and can be iterated over.
We can use break and continue in a for statement just like we used them in a while loop previously. We can also attach an else to a for loop in Python which will, just like with the while loop, only execute if a break statement is not encountered:
for i in range(1,5):
print(i)
if i % 7 == 0:
print('multiple of 7 found')
break
else:
print('no multiples of 7 in the range')
1
2
3
4
no multiples of 7 in the range
We got the output above because no multiple of 7 was found in the iterable range(1,5) which yielded iterated values of 1, 2, 3, and 4, respectively. Since the break statement was not encountered, the else block was executed.
Something worth remarking on is how to get at indexes for indexed iterables (e.g., lists, tuples, and strings are indexed iterables while, for example, sets and dictionaries are not). To illustrate, you might normally iterate through a string like so:
s = 'hello'
for c in s:
print(c)
But, of course, c here refers to the item being iterated from the iterable. Not the index of the item. We could get at this index in the following way:
s = 'hello'
i = 0
for c in s:
print(i,c)
i += 1
Sure, this works, but it's kind of annoying. We can use something a little similar:
s = 'hello'
for i in range(len(s)):
print(i, s[i])
This also works, but there is a better way of going about this.
s = 'hello'
for i, c in enumerate(s):
print(i, c)
Note that the built-in function enumerate returns a tuple where the first element of the tuple is an index while the second element of the tuple is the actual value that we are getting back from the iteration.
Classes
We can create a class in Python using the class keyword, but we need an initializer (i.e., a way to initialize or create an instance of our class). This is done or implemented in Python using the __init__ method. This method runs once the object has been created--so there are actually two steps when we create an instance of a class. We first have this "new" step (i.e., creation of a new object), but then the initializer is a step after that. After the object has been created, we can go on to the initialization phase.
So what happens in Python with these instance methods is that the first argument of the method is the object itself. So our first argument is going to be the object itself, and this is conventionally denoted by self, but you can call it anything you like:
class Rectangle:
def __init__(new_object_that_was_just_created, ...)
But it is customary to use self to denote the instance or object just created. For the Rectangle class we're going to require a width and height:
class Rectangle:
def __init__(self, width, height):
We are now going to set properties or attributes of the class--in this case they are going to be value attributes so we call them properties as opposed to methods which are callables essentially:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
It's worth noting that Python takes care of actually passing self to __init__ upon class instantiation. This is not something we have to do ourselves.
To clearly illustrate everything described about __init__ and self so far, consider the following code block:
object_set_atts = set(dir(object))
class Rectangle:
def __init__(self, width, height):
print('----- SELF OBJECT IN MEMORY -----')
print(self, end='\n\n')
print('----- DEFAULT OBJECT ATTRIBUTES -----')
print(object_set_atts, end='\n\n')
print('----- SELF OBJECT ATTRIBUTES BEFORE MODIFICATION -----')
print(set(dir(self)), end='\n\n')
print('ATTRIBUTES IN SELF NOT IN OBJECT')
print(set(dir(self)).difference(object_set_atts), end='\n\n')
print('ATTRIBUTES IN OBJECT NOT IN SELF')
print(object_set_atts.difference(set(dir(self))), end='\n\n')
self.width = width
self.height = height
print('ATTRIBUTES IN SELF NOT IN OBJECT AFTER ASSIGNMENT')
print(set(dir(self)).difference(object_set_atts), end='\n\n')
my_rect = Rectangle(4,6)
print(issubclass(Rectangle, object))
We get the following as output:
----- SELF OBJECT IN MEMORY -----
<__main__.Rectangle object at 0x10cbadfd0>
----- DEFAULT OBJECT ATTRIBUTES -----
{'__sizeof__', '__eq__', '__init__', '__gt__', '__lt__', '__reduce_ex__', '__le__', '__subclasshook__', '__class__', '__ge__', '__delattr__', '__ne__', '__dir__', '__repr__', '__init_subclass__', '__setattr__', '__reduce__', '__getattribute__', '__doc__', '__format__', '__str__', '__hash__', '__new__'}
----- SELF OBJECT ATTRIBUTES BEFORE MODIFICATION -----
{'__sizeof__', '__eq__', '__init__', '__gt__', '__lt__', '__reduce_ex__', '__le__', '__subclasshook__', '__class__', '__ge__', '__delattr__', '__ne__', '__dir__', '__dict__', '__repr__', '__init_subclass__', '__module__', '__setattr__', '__reduce__', '__getattribute__', '__doc__', '__format__', '__weakref__', '__str__', '__hash__', '__new__'}
ATTRIBUTES IN SELF NOT IN OBJECT
{'__module__', '__dict__', '__weakref__'}
ATTRIBUTES IN OBJECT NOT IN SELF
set()
ATTRIBUTES IN SELF NOT IN OBJECT AFTER ASSIGNMENT
{'height', '__weakref__', '__dict__', '__module__', 'width'}
True
Some points worth noting:
- dir: Concerning
dir, recall that if no argument is passed, thendir()returns the list of names in the current local scope (namespace). When anyobjectwith attributes is passed todir([object])as an argument,dir(object)returns the list of attribute names associated with thatobject. Its result includes inherited attributes, and is sorted. So the line at the beginning of the code block,object_set_atts = set(dir(object)), simply returns a set (the returned list is turned into a set to facilitate set operations) of the attribute names associated with the baseobjectclass. selfbefore modification: We initialize an instance of theRectangleclass by means of the linemy_rect = Rectangle(4,6). TheRectangle's__init__method fires, and we immediately see how Python passed in the newly createdselfobject to the__init__method and where it lives in memory:<__main__.Rectangle object at 0x10cbadfd0>. We then see all the attributes that are part of the baseobjectclass and howselfclearly inherits everything from this class and then more upon class instantiation. Specifically, attributes that are part of our newly createdselfobject that are not part of the baseobjectclass are__module__,__dict__, and__weakref__.selfafter slight modification: Once we declareself.width = widthandself.height = heightinside__init__and then compareselfwith the baseobjectclass, we see thatselfhas more attributes now:heightandwidth. This should be expected.Rectangleis subclass ofobject: Finally, once an instance of ourRectangleclass has been instantiated, we test whether or notRectangleis a subclass of the baseobjectclass. It is.
Let's now consider adding attributes which are callables (i.e., also known as "methods"). Specifically, let's add an area method and see what our Rectangle instance looks like:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
my_rect = Rectangle(4,6)
print(dir(my_rect))
This gives us the following:
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'area', 'height', 'width']
Worth noting here is how the listing of attributes for the my_rect instance differs compared to our previous listing of self in the __init__. If we modify the code block above to be
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
print(dir(self))
return self.width * self.height
my_rect = Rectangle(4,6)
print(dir(my_rect))
print(my_rect.area())
then we get the following:
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'area', 'height', 'width']
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'area', 'height', 'width']
24
Note that what all is printed out for my_rect and self within the area method is the same. It's also worth noting why, when methods depend on properties, we do not have to pass those properties explicitly to the method since the self object has these properties. That is, we can write
def area(self):
return self.width * self.height
as opposed to
def area(self, width, height):
return self.width * self.height
or some alternative even though the area method depends on those values. Those properties or values need to exist on the self object! And they do by means of the initializer __init__.
Now consider an updated version of the Rectangle class:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
r1 = Rectangle(10,20)
print(str(r1))
Python allows us to often print objects off as strings. What happens if we run print(str(r1))? We'll get something like <__main__.Rectangle object at 0x102ad5fd0>. But this is not a very informative or useful format unless we are interested in what kind of object we have and at what memory address. We could, of course, make our own "to string" method:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
def to_string(self):
return 'Rectangle: width={0}, height={1}'.format(self.width, self.height)
r1 = Rectangle(10,20)
and call it accordingly: print(r1.to_string()). But this is kind of annoying. It would be nice if we could use the built in str method. How could we do that? This is where Python is really nice in how it allows us to "overload" functions and methods. For example, what does str mean? By default, str is just going to look at the class and the memory address of the object. So how do we essentially override this and write our own definition for str?
It's very simple. We have these special methods that some call "magic" methods, but there's nothing really magical about them. They're well-documented and they're well-known. The special method name we need to use here is __str__. We can adjust our code accordingly:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
def __str__(self):
return 'Rectangle: width={0}, height={1}'.format(self.width, self.height)
r1 = Rectangle(10,20)
If we ran the above in a Python interactive shell, and then just entered r1, then we would see something like <__main__.Rectangle object at 0x10f926130> printed to the console (not str(r1)). If we want to change this behavior, then we need to implement another special method, namely the repr method. Just as str(object) is a built in function, repr(object) is a built in as well:
repr(object)returns the lower-level "as-code" printable string representation ofobject. The string generally takes a form potentially parseable byeval(), or gives more details thanstr().
So we could adjust our Rectangle class further to define how repr should work. Just as we modified __str__ to specify how str should work with an instance of the Rectangle class, we could modify __repr__ to specify how repr should work with an instance of the Rectangle class. As might be guessed by its name, __repr__ essentially stands for "representation" and the representation, if possible, is typically a string that shows how you would build the object up again. In some cases, there are too many variables and you can't really do it effectively, but we can in our case. So we can update our Rectangle class like so:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
def __str__(self):
return 'Rectangle: width={0}, height={1}'.format(self.width, self.height)
def __repr__(self):
return 'Rectangle({0}, {1})'.format(self.width, self.height)
r1 = Rectangle(10, 20)
So if we now entered r1 in an interactive Python shell session, we would get Rectangle(10, 20).
What about testing for equality? If we ran
r1 = Rectangle(10, 20)
r2 = Rectangle(10, 20)
print(r1 == r2)
we would get False as the output. r1 and r2 occupy different memory addresses. But as a user of the Rectangle class, you would really like to consider r1 and r2 as defined above to be equal. How can we make this happen? We can do this by means of another special nethod, namely __eq__. This allows us to specify and define how we compare objects to each other:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self.width, self.height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self.width, self.height)
def __eq__(self, other):
return self.width == other.width and self.height == other.height
# return (self.width, self.height) == (other.width, other.height)
r1 = Rectangle(10, 20)
r2 = Rectangle(10, 20)
print(r1 == r2)
Now the output would be True. The last line
return (self.width, self.height) == (other.width, other.height)
is simply another way of making the comparison. If we ran r1 is not r2 then we would get True, and this makes sense because different memory addresses are being occupied, but r1 == r2 now returns True as desired. What is not as desired is if we did something like r1 == 100. We would get an AttributeError since __eq__ for the Rectangle class is trying to find the height and width attributes for the other argument, which is provided as 100 in this case. And of course integers don't have such properties! So we need to make sure other is actually a Rectangle class instance:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self.width, self.height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self.width, self.height)
def __eq__(self, other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
This is now a bit cleaner. We can write all sorts of different kinds of comparison checks for our class (e.g., less than, great than, etc.). In fact, let's write a "less than" one which we define as one rectangle being less than another when its area has a smaller quantity:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self.width, self.height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self.width, self.height)
def __eq__(self, other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
def __lt__(self, other):
if isinstance(other, Rectangle):
return self.area() < other.area()
else:
return NotImplemented
What would then be the output from running
r1 = Rectangle(10, 20)
r2 = Rectangle(100, 200)
print(r1 == r2)
print(r1 < r2)
print(r1 > r2)
We would get
False
True
False
Why does the comparison r1 > r2 not throw an error? What happens is Python calls the __gt__ method for r1. It wasn't implemented. So what it does for us is it basically flips the comparison around and asks what r2 < r1 might be. Since __lt__ is implemented, we get False per the implementation of __lt__ in our Rectangle class.
Let's now consider a somewhat pared down version of the Rectangle class:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self.width, self.height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self.width, self.height)
def __eq__(self, other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
r1 = Rectangle(10, 20)
print(r1.width)
r1.width = -100
print(r1.width)
What would we get from running the above code? We would get
10
-100
The point is that we are allowing direct access to the width property as well as the height property; users can get as well as set the width and height for any given rectangle. But we may want to put logic in our code to prevent people from being able to give a rectangle a non-positive width or height. The way we prevent behavior likes this in Python (and in many other languages) is we define so-called getter and setter methods.
Our updated code with getter and setter methods for width and height might look like the following:
class Rectangle:
def __init__(self, width, height):
self._width = width
self._height = height
def get_width(self):
return self._width
def set_width(self,width):
if width <= 0:
raise ValueError('Width must be positive.')
else:
self._width = width
def get_height(self):
return self._height
def set_height(self,height):
if height <= 0:
raise ValueError('Height must be positive.')
else:
self._height = height
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self._width, self._height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self._width, self._height)
def __eq__(self, other):
if isinstance(other, Rectangle):
return self._width == other._width and self._height == other._height
else:
return False
Note the general change from self.width and self.height to self._width and self._height, respectively. This is to indicate that width and height should be considered as private variables. Of course, if we made such a change as we did above when our application was in production and many of our team members might be using the Rectangle class, then that would break a ton of code. As such, it is not a bad idea to generally start by defining private variables and using setters and getters from the beginning. The setters and getters will often be super basic such as
def get_width(self):
return self._width
def set_width(self, width):
self._width = width
You simply make modifications as you move along in your project. This is the typical of way doing this if you come from something like a Java background. In Python, this whole business of starting like that (i.e., by writing getters and setters from the beginning) does not really matter. Let's look at the Pythonic way of doing this. Let's go back to our original class:
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self.width, self.height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self.width, self.height)
def __eq__(self, other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
So we can read and set width and/or height however we please (just as before). Let's say this is what we released into production. But now we want to change this behavior. What's the solution? The solution is as expressed before in terms of writing a setter and getter, but we want to do this without breaking our backward compatibility. Python allows us to do this. That is why we do not have to start by writing getters and setters right away. In Python, unless you know you have a specific reason to implement a specific getter or setter that has extra logic, then you do not implement them. You just leave the properties bare. Remember that no variable is truly private in Python. And don't force people to use a getter or setter unless they have to. In Python, what happens is they're not really even aware that they're using a getter or setter.
How do we do this? We can use decorators to our advantage (to be discussed more later). Our new class might look like the following:
class Rectangle:
def __init__(self, width, height):
self._width = width
self._height = height
@property
def width(self):
return self._width
@width.setter
def width(self, width):
if width < 0:
raise ValueError('Width must be positive.')
else:
self._width = width
@property
def height(self):
return self._height
@height.setter
def height(self, height):
if height < 0:
raise ValueError('Height must be positive.')
else:
self._height = height
def __str__(self):
return "Rectangle: width={0}, height={1}".format(self.width, self.height)
def __repr__(self):
return "Rectangle({0}, {1})".format(self.width, self.height)
def __eq__(self, other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
r1 = Rectangle(10, 20)
print(r1.width)
r1.width = -100
print(r1.width)
Note how backward compatibility is preserved even if we change what is going on in the initializer. The reason the other methods still work is because when we call something like self.width from within __str__ we are actually calling the getter we just defined.
Even within our new __init__ method we could have self.height = height which would call the height setter to implement the restrictive logic we might want; otherwise, we could have something like r1 = Rectange(-100,10) happening for the class defined above. We don't want to allow that. So our __init__ method could go back to what we had before where the assignments would use the setter methods:
def __init__(self, width, height):
self.width = width
self.height = height
This results in now calling the setter methods for both width and height.
Variables and memory
Variables are memory references
Variables are memory references. We can think of memory as a series of slots or boxes that exist in our computer from which we can store and retrieve data:

We can also compare it to the mail system where you always have to write an address on your letter so it can be effectively delivered. It's pretty much the same in computers where we need addresses atached to our memory slots. We need memory addresses and they can be numbered rather arbitrarily:
When we actually store data in memory addresses, we may need more than one shelf or address in which to store an object (everything in Python is an object):
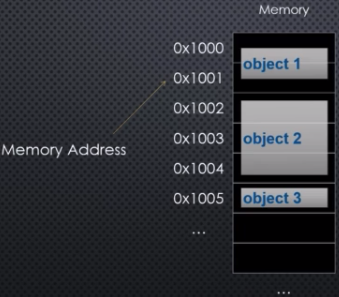
As long as we know where an object starts in memory, that is good enough. And this is called the heap. Storing and retrieving objects from the heap is taken care of for us by something called the Python memory manager.
To see how this works, consider what happens when you declare a variable as simple as the following:
my_var_1 = 10
When you execute this statement, the first thing Python does is create an object somewhere in memory, at some address, say 0x1000, and it stores the value 10 inside that object. And my_var_1 is simply a name, an alias if you will, for the memory address where that object is stored (or the starting address if it overflows into multiple slots). So my_var_1 is said to be a reference to the object at 0x1000. Note that my_var_1 is not equal to 10. In fact, my_var_1 is equal to 0x1000 in this case. But 0x1000 actually represents the memory address of the data we are interested in. So, for all practical purposes, my_var_1 is equal to 10. This is how we think about it.
Similarly, if we write my_var_2 = 'hello', then my_var_2 gets stored somewhere in memory, say at address 0x1002. If it overflows that's fine. Now my_var_2 now becomes an alias or reference to the memory address 0x1002 that represents the data we are interested in, namely the object which is the string 'hello'.
This can be largely summed up in a picture:

It's rather important to understand that variables in Python are always references. And they're references to objects in memory.
In Python, we can find the memory address referenced by a variable by using the id() function. This will return a base-10 number. We can convert this base-10 number to hexadecimal by using the hex() function.
The id function is not something you will typically be using as you write Python programs. But we will use it quite a bit in order to understand what's happening in the Python programs we run and especially what happens to variables as we pass them along in our code throughout their lifetime.
If we run something like
my_var = 10
print(my_var)
then we will get what we expect: 10. What actually happened is that Python looked at my_var, it then looked at what memory address my_var was referencing, it found that memory address, it went to the memory address, retrieved the data from memory, and then brought it back so we can display it in our console.
Bottom line: Variables are just references to memory addresses. They're not actually equal to the value we think they are. Logically, we can think of it that way. But in real terms they're memory references.
Reference counting
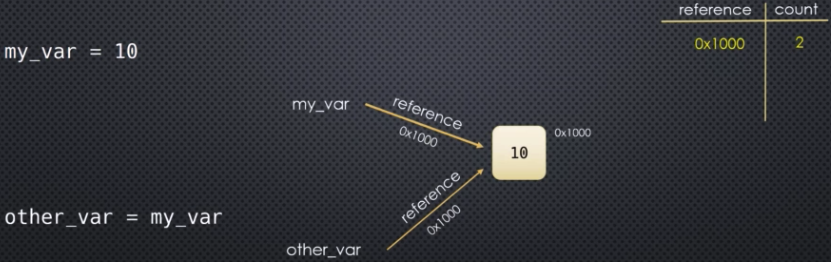
If we write the line of code my_var = 10 remember what is actually happening: Python is creating an object with an integer value of 10 at some memory address, say 0x1000 in this case. my_var is a pointer to that object--it is the reference or memory address of that object. So we can start keeping track of these objects that are created in memory. We can keep track of them by keeping track of their memory address and how many variables are pointing to them. How many other variables in our code are pointing to that some object?
Right now it's pretty clear when we declare my_var = 10 that our reference count is 1 for the memory address holding the integer value 10 referenced by my_var. But we could then write something like other_var = my_var. Remember that we are dealing with memory addresses and references. When we say other_var = my_var, we are not taking the value of 10 and assigning it to other_var--we're actually taking the reference of my_var and assigning that reference, 0x1000 in this case, to other_var. In other words, other_var is also pointing to that same object in memory (i.e., the integer value 10 being stored at memory address 0x1000).
It's important to understood the distinction outlined above. We do not have two separate objects of value 10, where my_var points to one and other_var points to another. No, when we say other_var = my_var, we're actually sharing the reference. So the reference count will go up to 2 in this case:
Let's now say my_var goes away. Maybe it falls out of scope or we assign it to a different object in memory (maybe even None). Then that reference goes away and the reference count goes down to 1. Let's now say other_var goes away. Maybe it too falls out of scope. Now there is nothing left and the reference count falls down to 0. At that point, the Python memory manager recognizes this and throws away the object if there are no references left. Now the previously occupied space in memory can be reused.
The whole process outlined above is called "reference counting" and is something the Python memory manager does for us. We don't have to worry about this since Python is doing it for us automatically. But it is valuable to know how Python is managing things behind the scenes. Garbage collection is related to this.
Before going into the code, we'll look at how we can find the reference count of a variable in Python. The sys module has a getrefcount function that we can use:
sys.getrefcount(my_var)
What's happening here is we are passing to sys.getrefcount a reference to my_var. So when we pass my_var to getrefcount we are actually creating another reference to that same object in memory. So there's kind of a downside to using this method because it always increases the reference count by 1 because simply the act of passing my_var to the function sys.getrefcount creates another reference to that same variable because variables are passed by reference in Python.
There is another function we can use that does not have this drawback:
ctypes.c_long.from_address(address).value
The difference here is that we are passing the memory address or id(my_var) (an integer, not a reference). Because we are passing the memory address, not the reference, the actual integer value, say 0x1000 in the previous example, this does not impact the reference count. This is a truer, more exact count of the number of references.
Consider this example:
import sys
a = [1,2,3]
print(sys.getrefcount(a)) # 2
As noted above, sys.getrefcount expects a variable name, a in our case. What this means is that we are passing a to getrefcount and its argument is taking the same reference that a is telling it--so it's going to point to the same object in memory. So really our reference count is going to become 2 when sys.getrefcount runs. Using this function is not an issue--just remember to subtract 1 because the simple act of passing a into sys.getrefcount has increased the reference count by 1.
To avoid this, we can import the ctypes module:
import ctypes
a = [1,2,3]
def ref_count(address: int):
return ctypes.c_long.from_address(address).value
print(ref_count(id(a))) # 1
Note how we have created a wrapper function ref_count to make our lives easier. This might seem odd at first given the problem we encountered when passing sys.getrefcount the variable a as an argument. Do we not encounter the same problem here when passing id the variable a as its argument? Clearly not. But why not? What's happening is id(a) is getting evaluated first. So, indeed, when we call id(a), when id is running, then the reference count of a is 2; but then id finishes running and returns the memory address of what variable a is pointing to. So by the time we call ref_count the id function has finished running and has released its pointer to the memory addressed referenced by its argument a. So that pointer reference is gone and the reference count is back down to 1 now.
Let's now make the assignment b = a and see what ref_count gives us:
import ctypes
a = [1,2,3]
b = a
def ref_count(address: int):
return ctypes.c_long.from_address(address).value
print(ref_count(id(a))) # 2
We can continue in this fashion, assigning other things to a and then changing the assignments:
import ctypes
def ref_count(address: int):
return ctypes.c_long.from_address(address).value
a = [1,2,3]
print(ref_count(id(a))) # 1
b = a
print(ref_count(id(a))) # 2
c = b
print(ref_count(id(a))) # 3
b = 10
print(ref_count(id(a))) # 2
You need to be very mindful when dealing directly with memory references in Python. Why? Take an example where you set a variable to None. The Python memory manager will free up that address which will become available for something else. Working with memory addresses may come up when debugging or dealing with memory leaks, but you will often not do this. It is helpful to know how Python really works behind the scenes though.
Garbage collection is related to reference counting, but it is not the same. It is a different process that Python utilizes to keep up with cleaning up the memory and keeping things freed up so we don't have memory leaks.
Garbage collection
Recall what reference counting is: As we create objects in memory, Python keeps track of the number of references we have to those objects. It could any number of references, but no matter what number of references we have, as soon as that reference count hits 0, the Python memory manager then destroys that object and reclaims the memory. So this is called reference counting. But sometimes that is not enough--it just doesn't work. In particular, we have to look at situations that can arise from so-called circular references. So what are circular references? Let's take a look at an example.
Suppose we have some variable my_var, and let's say my_var points to object A. So far so good--it's exactly what we've seen and the way in which Python normally operates. If my_var goes away or we point it to another object or None, then the reference count of object A goes from 1 to 0, and the Python memory manager at that point destroys object A and reclaims the space in memory. But let's suppose that object A has an instance variable, say var_1, that points to another object, say object B:

At this point, what happens if we get rid of the my_var pointer? Let's say we point it to None. Then the reference count of object A goes down to 0. The reference count of object B is still 1 since object A is pointing to object B. But the reference count for object A has just gone down to 0. Due to how reference counting works, object A will get destroyed. Once object A gets destroyed, object B's reference count also goes down to 0, and then it gets destroyed as well. So by destroying my_var, by removing that reference, the Python memory manager, through reference counting, will get rid of object A and B.
But now let's suppose object B also has an instance variable, say var_2, where var_2 points back to object A:
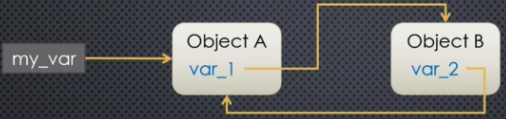
Now we have a circular reference. So what happens if we get rid of the my_var reference? If that goes away then the reference count for object A goes from 2 to 1. And the reference count for B stays at 1 since A is pointint to B. So in this case reference counting is not going to destroy either A or B. It can't. Because they both have references. They both have a reference count that is non-zero. And that is called a circular reference. And because the Python memory manager cannot clean that up, if we were to leave things as is, we would have a memory leak. This is where the garbage collector comes in.
The garbage collector will look and will be able to identify these circular references and clean them up. And so the memory leak goes away. The garbage collector can be controlled programmatically using the gc module. By default, the garbage collector is turned on. You can turn it off, but you really shouldn't unless you truly know what you are doing. Why would you want to turn it off? Mostly to free up some memory--the garbage collector obviously has to run (i.e., take up some space in memory) in order to collect and destroy the garbage. You can also call the garbage collector manually and interact with it and do your own cleanup. For now, just know the garbage collector is really there to clean up weak references and you should really leave it on unless you have very good reason to turn it off.
In general, the garbage collector works just fine, but as always there's a caveat. It doesn't always work, but this really applies to Python versions of less than 3.4. So if you're using Python 3.4+ then you should be fine. What was happening before is that if even one of the objects in the circular references had a destructor (e.g., __del__ ) then the order of the destructors might be important even though the garbage collector does not know what the order should be. So the obejct(s) would be marked as uncollectable. When you have that situation with a circular reference, where at least one of the objects had a destructor, then they weren't getting cleaned up by either the garbage collector or by reference counting. So you'd end up with a memory leak. This particular problem no longer exists for Python 3.4+.
Let's now look at some code and put the garbage collector through its paces and look at some circular references. We're going to look at a method, object_by_id, that's going to dig into the garbage collector and it will tell us whether or not that object exists in the garbage collector, and we'll do that by means of memory addresses.
Our object_by_id method above will basically look at all objects being tracked by the garbage collector (by means of gc.get_objects()) and it will try to find the object we are interested in by comparing the ids. There's another way we can compare memory addresses and we'll get to that later.
The commented code below illustrates all of the important points:
import ctypes
import gc
def ref_count(address: int):
return ctypes.c_long.from_address(address).value
def object_by_id(object_id):
for obj in gc.get_objects():
if id(obj) == object_id:
return "Object exists"
return "Not found"
class A:
def __init__(self):
self.b = B(self)
print('A: self: {0}, b: {1}'.format(hex(id(self)), hex(id(self.b))))
class B:
def __init__(self, a):
self.a = a
print('B: self: {0}, a: {1}'.format(hex(id(self)), hex(id(self.a))))
# prevent circular references from being cleaned up
gc.disable()
# create circular references
# two references to A:
# my_var -- direct reference to A
# my_var.b.a -- reference from B to A (created upon instantation of B)
# one reference to B: my_var.b
my_var = A()
# two references to A with same location in memory
print('Direct reference from my_var to A: ', hex(id(my_var)))
print('Reference from B to A: ', hex(id(my_var.b.a)))
# one reference to B
print('Reference from A to B: ', hex(id(my_var.b)))
# assign memory locations to new variables and get count
a_id = id(my_var.b.a)
print('Count of references to A (my_var -> A): ', ref_count(a_id)) # 2 (two references to object A)
b_id = id(my_var.b)
print('Count of references to B (my_var -> A): ', ref_count(b_id)) # 1 (one reference to object B)
# remove direct reference to object A
my_var = None
# reference from object B to A still exists but is now inaccessible: my_var.b.a
print('Count of references to A (my_var -> None): ', ref_count(a_id)) # 1
# reference from object A to B exists but is now inaccessible: my_var.b
print('Count of references to B (my_var -> None): ', ref_count(b_id)) # 1
# check to see if references are in the garbage collector
print('Reference to A in garbage collector: ', object_by_id(a_id))
print('Reference to B in garbage collector: ', object_by_id(b_id))
print('>>>> garbage being collected')
gc.collect()
print('garbage collected <<<<<')
# check to see if references are in the garbage collector
print('Reference to A in garbage collector: ', object_by_id(a_id))
print('Reference to B in garbage collector: ', object_by_id(b_id))
Here's the output (with added newline spaces for clarity):
B: self: 0x108fc9fa0, a: 0x108fc9fd0
A: self: 0x108fc9fd0, b: 0x108fc9fa0
Direct reference from my_var to A: 0x108fc9fd0
Reference from B to A: 0x108fc9fd0
Reference from A to B: 0x108fc9fa0
Count of references to A (my_var -> A): 2
Count of references to B (my_var -> A): 1
Count of references to A (my_var -> None): 1
Count of references to B (my_var -> None): 1
Reference to A in garbage collector: Object exists
Reference to B in garbage collector: Object exists
>>>> garbage being collected
garbage collected <<<<<
Reference to A in garbage collector: Not found
Reference to B in garbage collector: Not found
The takeaway from all of this: It's helpful to know that the garbage collector is largely responsible for destroying circular references. You can turn the garbage collector off, but you should almost always have it turned on.
Dynamic vs static typing
Some languages are statically typed (e.g., Java, Swift, C++, etc.). Here's some Java for example:
String myVar = "hello";
We have the variable name myVar which is to be expected, but we also have a data type at the beginning of the variable declaration (i.e., String in this case). Finally, we have a value, the string literal "hello" in this case, that we're assigning to myVar. What happens under the hood is very similar to what happens in Python:

The main thing to note here is that we are associating a data type with the variable name. So later if we try to do something like
myVar = 10;
this will not work because myVar has been declared as a String and cannot be assigned the integer value 10. Only values of type String can be assigned to myVar. For example, later on in our code, we could do something like myVar = "abc";.
Python, in contrast, is dynamically typed. So the main difference between what we saw above and the following code in Python
my_var = "hello"
is that we are not specifying that my_var is of type string. The name my_var is just a reference, nothing more. It is a reference to an object, where that object currently happens to be a string object with a value of "hello", but the type is not attached to my_var. Late on, if we say my_var = 10, that is perfectly legal. All we are doing is creating an object in memory, an integer object with value 10, and we are changing the reference of my_var to point to that integer:

In effect, we may think that the type of my_var has changed. But not really. In Python, my_var never had a type to start off with. my_var was just a reference. What has changed is the type of the object that my_var was pointing to. We can use the built-in type() function to determine the type of the object currently referenced by a variable. But remember: variables in Python do not have an inherent static type or any type for that matter. Instead, when we call type(my_var), what really happens is Python looks up the object my_var is referencing and returns the type of the object at that memory location.
Variable re-assignment
Suppose we have my_var = 10. We already know what's happening. We have an object in memory that gets created at some memory address where this object has a type of integer a value of 10 and my_var is simply a reference to that object:

If we later write a line of code like my_var = 15, then we are not changing the value inside the object located at the memory address previously taken up with an object of type integer and value of 10. Instead, what's happening is that a new object, also of type integer but with a value of 15, is created at some different memory address. And the reference of my_var changes to this new object:
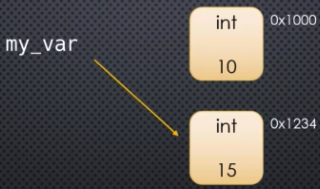
But note that the value of the object at memory address 0x1000, namely 10, does not change. The my_var reference simply no longer points to this value.
To further clarify how Python handles things, consider the following lines of code:
my_var = 10
my_var = my_var + 5
The same thing happens here. Don't be fooled. Don't think that because we have my_var on both sides of the expression that somehow something changes and now we're changing the value of the original object that my_var points to. We are not. Python first evaluates the right-hand side. First, Python looks at my_var and realizes it needs to add 5 to my_var. Okay, what's my_var? my_var is an integer with a value of 10. Well, 10 plus 5 is 15, and Python then creates a new object in memory at a different memory address with a value of 15. And then the my_var pointer is updated to point at or reference the new object and its value at this new memory address.
But we did not change the value of the contents or the state of the object at the original address my_var pointed to. In fact, the value inside the integer objects can never be changed.
Some of this is easier to see by means of code:
a = 10
print(hex(id(a)))
a = 15
print(hex(id(a)))
a = a + 0
print(hex(id(a)))
a = a + 1
print(hex(id(a)))
b = 16
print(hex(id(b)))
Here's the output:
0x108989a50 # a = 10
0x108989af0 # a = 15 (different address than above)
0x108989af0 # a = 15 (same address as above despite addition of 0)
0x108989b10 # a = 16 (different address than above)
0x108989b10 # b = 16 (same address as above)
Note how the memory address is the same for a and b when a = 16 and b = 16. So they both point to the same object in memory. There's a reason for this--that object's value can never change. That will be looked at in more detail later.
Object mutability
Consider some object in memory. Remember that an object is something that has a type and it also has some internal data--it has state. And it's located at some memory address. Changing the data inside the object is called modifying the internal state of the object. What's an example of this? Suppose we have a variable my_account that references some object in memory at some memory address, say 0x1000:

So the data type of our object is BankAccount and the object has two instance properties, the account number and the balance. Suppose we modify the balance in some way (payment or deposit):
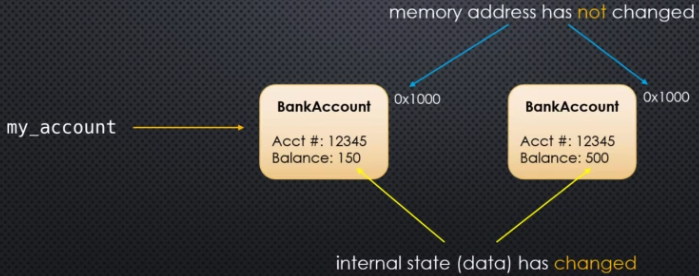
So the internal state (i.e., data) has changed. But the memory address has not changed. Previously, when we had my_var = 10 and then later changed this to my_var = 15, we ended up changing the reference; that is, the memory address that my_var pointed to changed but the object originally pointed to did not change. But now we are actually modifying the internal state of the same object. Integer objects are immutable and nothing about them can change--their internal state or data cannot be modified. An integer cannot change from, say, 7 to 8. But the reference we are using to point to an integer object can change. And that's usually what happens. But now we are looking at cases where the object we are pointing to can actually change or mutate. The memory address we are pointing to will not change, but the internal state of the object being pointed to can change.
A change as described above, where the object being referenced or pointed to has its internal state changed, is called a mutation. To say an object was mutated is just a fancy way of saying that the internal data of that object has changed. An object whose internal state can be changed is called mutable. An object whose internal state cannot be changed is called immutable (the object gets created in memory but we can never change the state of that object). These are different definitions we should keep in mind because they impact how we program. Let's look at some examples of immutables and mutables in Python:
| Immutable | Mutable |
|---|---|
Numbers (int, float, bool, complex, etc.) | Lists |
| Strings | Sets |
| Tuples | Dictionaries |
| Frozen sets | User-defined classes |
| User-defined classes (when no methods allow modification) |
Let's take a look at some finer points worth bearing in mind, namely how mutability and immutability can sometimes intermingle in potentially unexpected ways. Let's say we have a tuple:
t = (1, 2, 3)
Remember that tuples are immutable. Elements cannot be deleted, inserted, or replaced. In the case above, both the container (the tuple) and all its elements (ints) are immutable. So not much can be done in the way of intermingling mutability with immutability. But what if we now define mutable elements a and b that comprise a tuple t:
a = [1, 2]
b = [3, 4]
t = (a, b)
Can we change a and b and see those changes reflected in t?
Sure:
a = [1, 2]
b = [3, 4]
t = (a, b)
print(t)
# modify the elements of a and b in place
a.append(3)
a.extend([4,5,6])
b.append('lions')
b.extend(['bears', 'tigers'])
print(t)
Here's the output:
([1, 2], [3, 4])
([1, 2, 3, 4, 5, 6], [3, 4, 'lions', 'bears', 'tigers'])
The very important thing is that we modify a and b in place; that is, in order to see changes to lists a and b reflected in the tuple t, the memory addresses to which a and b point must remain the same. In fact, it may be helpful to view t as simply consisting of the memory addresses originally pointed to by a and b--the memory address of a is 0x123 and the memory address of b is 0x124, then t is basically a collection of just 0x123 and 0x124 and always will be (even if we modify the internal state or data of the objects residing at 0x123 and 0x124).
If we do something like a = a + a, then the new a formed by concatenating a with a will not point to the same memory address that the original a pointed to. The + operation for lists is not an in-place operation--this operation will concatenate two lists and return the newly concatenated list. The newly created list by concatenation will reside somewhere in memory different from the original a value.
This example should make all of this clear:
a = [1, 2, 3]
a_id = a
t = (a)
print('Memory address of a: ', hex(id(a)))
print('Memory address of a_id: ', hex(id(a_id)))
print('Tuple t: ', t)
a.append(4)
print('Memory address of a: ', hex(id(a)))
print('Memory address of a_id: ', hex(id(a_id)))
print('Tuple t: ', t)
a = a + [-2, -1]
a_id.extend([5, 6])
print('Memory address of a: ', hex(id(a)))
print('Memory address of a_id: ', hex(id(a_id)))
print('Tuple t: ', t)
Here's the output:
Memory address of a: 0x1088425c0
Memory address of a_id: 0x1088425c0
Tuple t: [1, 2, 3]
Memory address of a: 0x1088425c0
Memory address of a_id: 0x1088425c0
Tuple t: [1, 2, 3, 4]
Memory address of a: 0x1088ccb40
Memory address of a_id: 0x1088425c0
Tuple t: [1, 2, 3, 4, 5, 6]
Note how the memory address of a changes; that is, a = a + [-2, -1] results in a pointing to a different memory address than that which it originally pointed to. The memory address that a originally pointed to has been saved as a_id, and this reference never changes throughout the block of code above.
In summary, although the tuple t is immutable, the element residing within it (i.e., a) is not. The object reference in the tuple did not change (i.e., the original memory address pointed to by a), but the referenced object did mutate (not by a = a + [-2, -1] but by a_id.extend([5, 6])).
Function arguments and mutability
We are going to look at how our variables may or may not be effected by functions when we call them and pass our variables to them. Mutability and immutability are really important in this context.
Recall from before that, for example, strings (str) are immutable objects in Python. Once a string has been created, the contents of the object can never be changed. If we write my_var = 'hello', then the only way to modify the "value" of my_var is to re-assign my_var to another object.
In general, immutable objects are safe from unintended side-effects. And by side-effects we mean that when we call a function with our variable, then that function may or may not alter the value of that variable. If we have immutable objects, then we have a general amount of safety.
Suppose we have a function process that takes in a parameter s:
def process(s):
s = s + " world"
return s
And let's say in our main code we have my_var = "hello". In this example, we basically have two scopes:
modulescopeprocessscope
When we run my_var = "hello" the module scope has a variable called my_var and it points to some object in memory, namely the immutable string object "hello" in this case. When we run process(my_var), we are calling the process function and we are passing my_var as the argument. This next part is critically important to understand: my_var's reference is passed to process():

So my_var's reference, 0x1000 in this case, is passed to process, and the process scope now stores that reference in the variable s (i.e., the function parameter). So s points to the same object that my_var points to, namely the object residing at memory address 0x1000. When the piece of code s = s + " world" runs, we are not going to be modifying the contents of the object at memory address 0x1000--the object that lives there is immutable. We can't modify it. So the only way that s can now be equal to "hello world" is for us to create a new object in memory at some different memory address. Then the reference of s inside the process scope will change to point to this new object. But in the module scope, the my_var reference does not change. It still points to the object at memory address 0x1000, namely the immutable object of type str with value "hello".
So when we print my_var after the process function has run, we will still get "hello". The object my_var serves as a reference to has not changed because it cannot change. As can be seen from this example, because the string is immutable, we have some safety here. More generally, we can see how immutable objects are safe from unintended side effects.
Of course, the flipside of all this is what happens when we have mutable objects. Suppose we update the process function to deal with lists:
def process(lst):
lst.append(100)
And let's say in our module code we have my_list = [1, 2, 3]. In the module scope, my_list points to an object in memory, again let's say 0x1000. When we call process(my_list), we're again essentially passing the my_list reference to process. Now, in the process scope, lst points to the same object that my_list points to. Nothing has changed so far from this example to the previous example with the string. But when we run lst.append(100) inside the process method, we append 100, but what object are we appending 100 to? The object that lst currently points to which is the same object that my_list points to. Hence, the object at 0x1000 has its internal state changed--the object is mutated. The memory address has not changed. It's the same object. We have simply changed its state. So when print my_list after running process(my_list), we will get [1, 2, 3, 100].
Shared references and mutability
The term shared reference is the concept of two variables referencing the same object in memory (i.e., having the same memory address). For example, if we write a = 10, then we can create a shared reference by declaring another variable like so: b = a. Now b and a both point to the same memory address. Shared references are also created all the time when a function is called that accepts different arguments--those arguments will have their module scope and shared references with local scope (to the calling function) are created for each argument (remember that arguments are passed by reference to functions).
So the shared reference model looks somewhat like the following:
The following may be somewhat surprising. If we write a = 10 and b = 10, then we might expect for a and b to point to different objects in memory. But they don't. Similarly, if we write s1 = "hello" and s2 = "hello", then s1 and s2 will both point to the same object in memory:
This is due to the fact that, in both cases, we are referencing immutable objects in memory. They are safe from unintended side-effects. Python's memory manager decides to automatically re-use the memory references for optimization reasons--we'll look at this in more detail soon. Is the re-using of of memory references safe? Yes, since they are immutable.
We have to be more careful with mutable references though, especially when those mutable references contain nested objects. To truly see this in action, consider the following code block:
import copy
# integers (immutable)
n1 = 10
n2 = n1
# strings (immutable)
s1 = "hello"
s2 = s1
# lists (mutable)
l1 = [1, [2, 3]]
l2 = l1
l3 = l1[:]
l4 = l1.copy()
l5 = [*l1]
l6 = list(l1)
l7 = copy.deepcopy(l1)
l1[1].append(100) # modify nested object in place
# dictionaries (mutable)
d1 = {"key1": "value1", "key2": {"key2a": "value2a", "key2b": [1, 2, 3]}}
d2 = d1
d3 = d1.copy()
d4 = {**d1}
d5 = dict(d1)
d6 = copy.deepcopy(d1)
d1['key2']['key2a'] = 'NEW VALUE IN NESTED ITEM' # modify nested object in place
# inspect
print("n1: ", hex(id(n1)))
print("n2: ", hex(id(n2)))
print("s1: ", hex(id(s1)))
print("s2: ", hex(id(s2)))
print("l1: ", hex(id(l1)))
print("l2: ", hex(id(l2)))
print("l3: ", hex(id(l3)))
print("l4: ", hex(id(l4)))
print("l5: ", hex(id(l5)))
print("l6: ", hex(id(l6)))
print("l7: ", hex(id(l7)))
print("l1, item 2: ", hex(id(l1[1])))
print("l2, item 2: ", hex(id(l2[1])))
print("l3, item 2: ", hex(id(l3[1])))
print("l4, item 2: ", hex(id(l4[1])))
print("l5, item 2: ", hex(id(l5[1])))
print("l6, item 2: ", hex(id(l6[1])))
print("l7, item 2: ", hex(id(l7[1])))
print("l1, final: ", l1)
print("l2, final: ", l2)
print("l3, final: ", l3)
print("l4, final: ", l4)
print("l5, final: ", l5)
print("l6, final: ", l6)
print("l7, final: ", l7)
print("d1: ", hex(id(d1)))
print("d2: ", hex(id(d2)))
print("d3: ", hex(id(d3)))
print("d4: ", hex(id(d4)))
print("d5: ", hex(id(d5)))
print("d6: ", hex(id(d6)))
print("d1, key 2: ", hex(id(d1['key2'])))
print("d2, key 2: ", hex(id(d2['key2'])))
print("d3, key 2: ", hex(id(d3['key2'])))
print("d4, key 2: ", hex(id(d4['key2'])))
print("d5, key 2: ", hex(id(d5['key2'])))
print("d6, key 2: ", hex(id(d6['key2'])))
print("d1, final: ", d1)
print("d2, final: ", d2)
print("d3, final: ", d3)
print("d4, final: ", d4)
print("d5, final: ", d5)
print("d6, final: ", d6)
Here's the output (newlines inserted for clarity):
n1: 0x105ebda50
n2: 0x105ebda50
s1: 0x106056a30
s2: 0x106056a30
l1: 0x1061e1080
l2: 0x1061e1080
l3: 0x1061e4580
l4: 0x1061e4540
l5: 0x1061f4900
l6: 0x1061f4bc0
l7: 0x1061f4ac0
l1, item 2: 0x1060be9c0
l2, item 2: 0x1060be9c0
l3, item 2: 0x1060be9c0
l4, item 2: 0x1060be9c0
l5, item 2: 0x1060be9c0
l6, item 2: 0x1060be9c0
l7, item 2: 0x1061f4980
l1, final: [1, [2, 3, 100]]
l2, final: [1, [2, 3, 100]]
l3, final: [1, [2, 3, 100]]
l4, final: [1, [2, 3, 100]]
l5, final: [1, [2, 3, 100]]
l6, final: [1, [2, 3, 100]]
l7, final: [1, [2, 3]]
d1: 0x105fdf180
d2: 0x105fdf180
d3: 0x1061d6500
d4: 0x1060be6c0
d5: 0x1061f4c80
d6: 0x1061f4a00
d1, key 2: 0x105fdf0c0
d2, key 2: 0x105fdf0c0
d3, key 2: 0x105fdf0c0
d4, key 2: 0x105fdf0c0
d5, key 2: 0x105fdf0c0
d6, key 2: 0x1061eb200
d1, final: {'key1': 'value1', 'key2': {'key2a': 'NEW VALUE IN NESTED ITEM', 'key2b': [1, 2, 3]}}
d2, final: {'key1': 'value1', 'key2': {'key2a': 'NEW VALUE IN NESTED ITEM', 'key2b': [1, 2, 3]}}
d3, final: {'key1': 'value1', 'key2': {'key2a': 'NEW VALUE IN NESTED ITEM', 'key2b': [1, 2, 3]}}
d4, final: {'key1': 'value1', 'key2': {'key2a': 'NEW VALUE IN NESTED ITEM', 'key2b': [1, 2, 3]}}
d5, final: {'key1': 'value1', 'key2': {'key2a': 'NEW VALUE IN NESTED ITEM', 'key2b': [1, 2, 3]}}
d6, final: {'key1': 'value1', 'key2': {'key2a': 'value2a', 'key2b': [1, 2, 3]}}
Several methods are included in the code above that illustrate the copying of a list or dictionary (two of the most frequently used mutable objects), but most of these methods result in a shallow copy. What actually is a shallow copy in Python? The easiest way to understand is to consult the documentation for the copy module:
Assignment statements in Python do not copy objects, they create bindings between a target and an object. For collections that are mutable or contain mutable items, a copy is sometimes needed so one can change one copy without changing the other. This module provides generic shallow and deep copy operations (explained below).
copy.copy(x): Return a shallow copy ofx.
copy.deepcopy(x[, memo]): Return a deep copy ofx.The difference between shallow and deep copying is only relevant for compound objects (objects that contain other objects, like lists or class instances):
- A shallow copy constructs a new compound object and then (to the extent possible) inserts references into it to the objects found in the original.
- A deep copy constructs a new compound object and then, recursively, inserts copies into it of the objects found in the original.
Two problems often exist with deep copy operations that don't exist with shallow copy operations:
- Recursive objects (compound objects that, directly or indirectly, contain a reference to themselves) may cause a recursive loop.
- Because deep copy copies everything it may copy too much, such as data which is intended to be shared between copies.
The
deepcopy()function avoids these problems by:
- keeping a
memodictionary of objects already copied during the current copying pass; and- letting user-defined classes override the copying operation or the set of components copied.
In addition to the details and documentation above, this thread on Stack Overflow may be helpful.
Variable equality
We can think of variable equality in two fundamental ways:
- memory address
- object state (data)
The distinction between these two ways of looking at variable equality can be easily seen as follows:
a = [1,2,3]
b = [1,2,3]
Are a and b equal? If we answer this question using memory addresses, then the answer is no. If we are talking about object state or data, then the answer is yes.
Python gives us a specific way of making these comparisons. When we want to use memory addresses for determining variable equality, we use the is identity operator: var_1 is var_2. This will tell us, by means of a returned boolean value of True or False, whether or not var_1 and var_2 point to the same memory address.
On the other hand, if we want to compare the internal state (i.e., data) of two objects, then we use the == equality operator: var_1 == var_2. This will tell you whether or not the contents of var_1 and var_2 are equal.
For negation, if you want to test whether or not the memory addresses of two variables are not equal, then you use is not: var_1 is not var_2. If you want to test whether or not two objects are not equal in terms of their content or internal state, then you can use !=: var_1 != var_2.
The None object is worth discussing momentarily. The None object can be assigned to variables to indicate that they are not set in the way we would expect them to be (i.e., an "empty" value or null pointer). But the None object is a real object that is measured by the Python memory manager. Furthermore, the memory manager will always use a shared reference when assigning a variable to None. So if you assign a bunch of variables to None, then all of those variables will point to the same memory address. We can test if a variable is "not set" or "empty" by comparing its memory address to the memory address of None using the is operator: a is None.
Everything is an object
We will encounter many data types throughout our work in Pythin:
- Integers (
int) - Booleans (
bool) - Floats (
float) - Strings (
str) - Lists (
list) - Tuples (
tuple) - Sets (
set) - Dictionaries (
dict) - None (
NoneType)
But we'll see other constructions as well:
- Operators (
+,-,==,is, ...) - Functions
- Classes
- Types
We'll see a lot more than just those things listed above, but even just the above items is enough to keep us occupied for quite some time. But the one thing in common with all these things is that they are all objects (instances of classes):
- Functions (
function) - Classes (
class) [not just instances but the class itself] - Type (
type)
This means they all have a memory address. In particular, functions have a memory address. And this will be really important to keep in mind. Consider the following code block:
def my_func():
pass
print(my_func)
print(hex(id(my_func)))
Here's the output:
<function my_func at 0x108dbdf70>
0x108dbdf70
The model looks kind of like this:
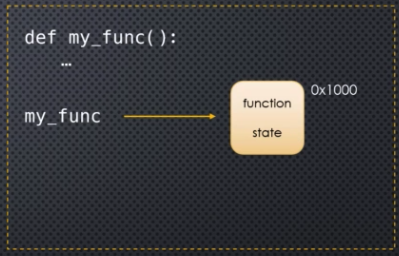
Hence, in this case, my_func is basically acting as we have seen variables names previously. But our variable in this case points to an object that exists at some memory address and has some state, where this state includes many things (e.g., the code that my_func comprises, what happens to variables as they get created within the my_func scope, etc., and all of that is bound to the function state). As also shown in the code block above, we can call id(my_func) just as we could call id(my_var) for variables we were previously considering. But now what we are looking at happens to be a function object as opposed to, say, an int object.
Any object can be assigned to a variable, including functions. And any object can be passed to a function, including other functions! This will be very useful when we are looking at things like decorators. Any object can also be returned from a function, including other functions!
As a side note it's worth observing how we can get help on many built-in objects that we might create. Doing something like a = 10 and then type(a) will return <class 'int'> which shows us that we are dealing with an instance of the int class. We can execute help(int) to get some documentation on this class. If we look at the documentation for int, then we can observe things like the following:
a = int()
b = int('101', base=2)
c = int('0b101', base=0)
d = int('0b100', base=0)
e = int('237', base=0)
print(a)
print(b)
print(c)
print(d)
print(e)
Our output:
0
5
5
4
237
Per the documentation provided by help(int), we see we have int([x]) -> integer and int(x, base=10) -> integer for the int class. More completely:
Convert a number or string to an integer, or return
0if no arguments are given. Ifxis a number, returnx.__int__(). For floating point numbers, this truncates towards zero.If
xis not a number or ifbaseis given, thenxmust be a string, bytes, or bytearray instance representing an integer literal in the given base. The literal can be preceded by'+'or'-'and be surrounded by whitespace. The base defaults to10. Valid bases are0and2-36. Base0means to interpret the base from the string as an integer literal.
Python optimizations: interning, string interning, and peephole
Much of what has been noted so far concerning memory management, garbage collection, and what we will now discuss regarding optimizations is usually specific to the Python implementation you use. Often you will be using CPython, the standard Python implementation written in C. But there are other Python implementations out there. For example:
- Jython: Written in Java and can import and use any Java class. It even compiles to Java bytecode which can then run in a JVM.
- IronPython: This is written in C# and targets >net (and mono) CLR
- PyPy: This is written in RPython (which is itself a statically-typed subset of Python written in C that is specifically designed to write interpreters)
Interning
It is possible for us to make assignments to the same immutable object in Python but end up with different memory addresses:
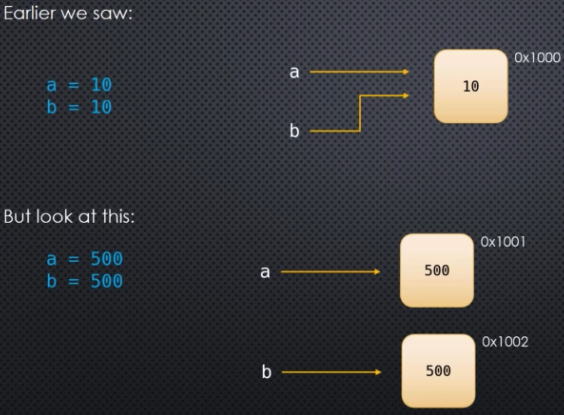
If we write a = 500 and b = 500 in our own module and then execute the code, we may actually end up with the same memory addresses for a and b seeming to contradict the picture above. Why? This is due to some optimization steps that happen during compilation. In this case, since the a and b symbols both point to a constant integer, Python's optimizer reuses the same object. But if you did this in two separate modules, you would see that a number such as 100 would still have the same memory address, but the number 500 would have different memory addresses. This link goes into a bit more detail, but it is rather hard to follow; the easiest way to understand what is going on is to look at a bit of code:
Suppose we have example.py with the following code:
# example.py
from mymodule import a2, b2, c2, d2, e2, f2
a1 = -5
b1 = 256
c1 = -6
d1 = 257
e1 = 10
f1 = 500
print('a1 and a2 (-5): ' , hex(id(a1)), hex(id(a2)))
print('b1 and b2 (256): ', hex(id(b1)), hex(id(b2)))
print('c1 and c2 (-6): ', hex(id(c1)), hex(id(c2)))
print('d1 and d2 (-257): ', hex(id(d1)), hex(id(d2)))
print('e1 and e2 (10): ', hex(id(e1)), hex(id(e2)))
print('f1 and f2 (500): ', hex(id(f1)), hex(id(f2)))
And the contents of mymodule.py:
# mymodule.py
a2 = -5
b2 = 256
c2 = -6
d2 = 257
e2 = 10
f2 = 500
Here is the output:
a1 and a2 (-5): 0x1039d0870 0x1039d0870
b1 and b2 (256): 0x103a00990 0x103a00990
c1 and c2 (-6): 0x103c98eb0 0x103c98e50
d1 and d2 (-257): 0x103b913f0 0x103c98f10
e1 and e2 (10): 0x1039d0a50 0x1039d0a50
f1 and f2 (500): 0x103c98ef0 0x103c98f50
What is going on here? Python practices something called interning: reusing objects on-demand. Specifically, at startup, Python (CPython) pre-loads (caches) a global list of integers in the range [-5, 256], inclusive. What that means is that any time an integer is referenced in that range (even from another module), Python will use the cached version of that object. Hence, in the code block above, a1 and a2, b1 and b2, and e1 and e2 share pairwise-equivalent memory addresses since they are referencing integer objects that are cached at startup--all of those values fall between -5 and 256, inclusive. The other pairs of values do not fall in that range and thus cannot rely on caching for optimization.
Essentially, the integers in the range from -5 to 256, inclusive, are singleton objects which are basically classes that can only be instantiated once. So whenever you try to reinstantiate them you just get the original version back. It's kind of the same thing that is happening here. What's the optimization strategy by Python? Small integers show up often.
When we write a = 10, Python simply has to point to the existing reference for 10. It doesn't have to create that integer object. If, however, we write something like a = 257, then we must note that this number falls outside the -5 to 256 range. So Python cannot use the global list and a new object must be created.
String Interning
Immediately above we saw interning introduced in the context of Python automatically interning a range of integers at startup. But interning occurs for more than just a small range of integers. Some strings are also automatically interned. But certainly not all! As the Python code is compiled, identifiers are interned (e.g., variable names, function names, class names, etc.). Your code largely consists of strings and much of that is interned. Some string literals may also be automatically interned:
- string literals that look like identifiers (e.g.,
"hello_world") - if it starts with a digit, even though that is not a valid identifier, it may still get interned
But don't count on the interning automatically happening! Python is doing this interning for a reason. Why? It's all about optimization (speed and memory). If you think about what is happening as your Python code is running, both internally, and in the code you write, deals with lots and lots of dictionary type lookups, on string keys, which means a lot of string equality testing. Let's say we want to see if two strings are equal:
a = 'some_long_string'
b = 'some_long_string'
Using a == b, we need to compare the two strings character by character. But if we know that 'some_long_string' has been interned, then a and b are the same string if they both point to the same memory address in which case we can use a is b instead which will compare two integers (memory addresses) and this is a faster comparison than character by character.
Not all strings are automatically interned by Python. But you can force strings to be interned by using the sys.intern() method:
import sys
a = sys.intern('the quick brown fox')
b = sys.intern('the quick brown fox')
Note that we cannot just do b = 'the quick brown fox'. That would create a new object in memory. But now we can use a is b for comparison which is much faster than running a == b. So the question becomes: When should you do this? In general, don't do it. Unless you have a specific need:
- dealing with a large number of strings that could have a high repetition (e.g., tokenizing a large corpus of text (NLP))
- lots of string comparisons
If we test out string interning, we will run into the same "problem" as we did earlier with integers in the sense that if we place everything in the same module, then interning will happen automatically for us even when it "shouldn't" simply because of some optimizations that the Python engine makes. But to really test things out, we can make an example.py file like so:
# example.py
import sys
from mymodule import a2, b2, c2, d2
a1 = 'some_string'
b1 = 'non identifier'
c1 = sys.intern('non identifier but interned across modules')
d1 = sys.intern('non identifier and not interned across modules')
print(a1 is a2)
print(b1 is b2)
print(c1 is c2)
print(d1 is d2)
And mymodule.py is like so:
# mymodule.py
import sys
a2 = 'some_string'
b2 = 'non identifier'
c2 = sys.intern('non identifier but interned across modules')
d2 = 'non identifier and not interned across modules'
The output:
True
False
True
False
This shows that Python will generally try to intern strings that look like identifiers but not other strings. Also, if you want to manually intern a string, then you need to use sys.intern on all instances of that string.
Peephole
Peephole optimizations are just another kind of optimization that can occur at compile time. Certain things get optimized. For example, consider constant expressions, something like where the numeric calculation 24 * 60 gets assigned to a variable. If this line of code gets executed many many times during the lifetime of our program, then Python is going to have to calculate 24 * 60 again and again and again.
We may be tempted as developers to simply write 1440, but this may be problematic in some cases (e.g., maybe 24 and 60 have meaning such as hours and minutes). But it would be nice to save some time by not having to calculate 24 * 60 every time, especially if we are seeing that computation come up a lot. It turns out Python will actually pre-calculate 24 * 60 -> 1440. So when your code gets compiled and while your code is running, references to 24 * 60 will be replaced by the pre-calculated value of 1440. The takeaway: Expressions that evaluate to a constant are pre-calculated and stored.
The same is true in a different ssense when it comes to short sequences (length less than 20). So something like (1, 2) * 5 = (1, 2, 1, 2, 1, 2, 1, 2, 1, 2) will be pre-calculated and stored. The same goes for 'abc' * 3 which would become 'abcabcabc'. And the same also goes for 'hello' + ' world' which would become 'hello world'. On the other hand, something like 'the quick brown fox' * 10 will not be pre-calculated and stored. The tradeoff for sequence types is 20 characers--this is what Python has decided is the cutoff in terms of what makes the storing worth it from a speed and memory perspective.
The next type of peephole optimization is membership testing: mutables are replaced by immutables. For example, if e in [1, 2, 3] is a membership test. The list [1, 2, 3] is actually treated as a constant while your code is running and the membership test is being made. The idea is that [1, 2, 3] is a string of code and you don't change your code while your program is running. This would not be true if the items in the list were also mutable (e.g., other variables that would change values). So basically when the constant, mutable expression (i.e., [1, 2, 3] in this case) is encountered, Python will replace it with its immutable counterpart. So [1, 2, 3] gets transformed into (1, 2, 3). In general, lists get converted to tuples, sets get converted to frozen sets, etc.
It's worth noting that set membership is much faster than list or tuple membership (sets are basically like dictionaries). So, instead of writing if e in [1, 2, 3] or if e in (1, 2, 3), you should think hard and probably write it like so: if e in {1, 2, 3}.
Apparently in Python 3.7+ the automatic string intern limit is set at 4096.
So the code
def my_func():
a = 24 * 60
b = (1, 2) * 5
c = 'abc' * 3
d = 'ab' * 11
e = 'the quick brown fox' * 5
f = ['a', 'b'] * 3
g = 'a' * 4097
print(my_func.__code__.co_consts)
will give the following output:
(None, 1440, (1, 2, 1, 2, 1, 2, 1, 2, 1, 2), 'abcabcabc', 'ababababababababababab', 'the quick brown foxthe quick brown foxthe quick brown foxthe quick brown foxthe quick brown fox', 'a', 'b', 3, 4097)
Note how all values for a-e are pre-calculated, but f and g are not precalculated (f due to the list being mutable and g due to exceeding the 4096 limit).
Now let's discuss membership testing and peephole optimization. Consider the following code:
def my_func(e, f):
if e in [1, 2, 3]:
pass
if f in {4, 5, 6}:
pass
print(my_func.__code__.co_consts)
This has the following output:
(None, (1, 2, 3), frozenset({4, 5, 6}))
So once the my_func function has been compiled, we see some constants that have been pre-calculated to be associated with that function, namely (1, 2, 3) and frozenset({4, 5, 6}). Note how these are the immutable variants of [1, 2, 3] and {4, 5, 6}, respectively. In general, when we do any list or sequence membership testing, the peephole optimizer is going to transform any kind of mutable element into an immutable version of that element when it can.
When it comes to membership testing, testing whether or not an element is in a set is almost always faster than testing whether or not the element is in a list or tuple. Note that sets are unordered. Consider the following block of code to illustrate this:
import string
import time
char_list = list(string.ascii_letters)
char_tuple = tuple(string.ascii_letters)
char_set = set(string.ascii_letters)
def membership_test(n, container):
for _ in range(n):
if 'z' in container:
pass
start_char_list = time.perf_counter()
membership_test(10000000, char_list)
end_char_list = time.perf_counter()
print(end_char_list - start_char_list)
start_char_tuple = time.perf_counter()
membership_test(10000000, char_tuple)
end_char_tuple = time.perf_counter()
print(end_char_tuple - start_char_tuple)
start_char_set = time.perf_counter()
membership_test(10000000, char_set)
end_char_set = time.perf_counter()
print(end_char_set - start_char_set)
start_char_to_list_to_set = time.perf_counter()
membership_test(10000000, set(list(string.ascii_letters)))
end_char_to_list_to_set = time.perf_counter()
print(end_char_to_list_to_set - start_char_to_list_to_set)
Here's the output for one sample run:
3.911477312
3.7336435709999996
0.3642787289999996
0.3585400000000014
Even when you have to convert the string of letters to a list and then to a set, the comparison is much faster.
Numeric types
Overview
We are now going to look at the numeric types in Python (so basically how we can represent numbers in Python). We have five main types of numbers:
| Number Type | Example | Python Internal Representation |
|---|---|---|
| Integer (Z) | ..., -2, -1, 0, 1, 2, ... | int |
| Rational (Q) | `{ p/q | p,q in Z, q != 0 }` |
| Real (R) | 0, -1, 0.125, pi, ... | float; decimal.Decimal |
| Complex (C) | `{ a + b*i | a,b in R }` |
| Boolean truth values | 1 (True), 0 (False) | bool |
Note that the bool data type exists for booleans, but under the hood we're really doing with a small subset of the integers, namely 0 and 1.
Integers - Data types
An integer in Python is of the int data type. For example: 0, 10, -100, 1000000, etc. Intuitively, we know what integers are. So the question becomes: How big can they become? How large can a Python int become (positive or negative)? To understand this, we really need to understand how integers are stored in a computer. Internally, integers are represented using base-2 digits (binary), not decimal (base-10).
As an example, the base-2 number 10011 is equivalent to the base-10 number 19 or perhaps more clearly: (10011)_2 = (19)_10. As we can see, it takes 5 bits to represent 19 in base 2.
What's the largest (base 10) integer number that can be represented using 8 bits? Right now let's just assume we care about non-negative integers. We'd have (1111 1111)_2 = 255 = 2^8 - 1. If we care about looking at negative integers, then we are going to need to use one of our bits as a sort of sign encoding. That is, if we about handling negative integers as well as positive integers, then 1 bit is reserved to represent the sign of the number, leaving us with only 7 bits for the number itself out of the original 8 bits. The largest number we can represent using 7 bits is 2^7 - 1 = 127. So, using 8 bits we are able to represent all the integers in the range [-127. 127]. Since 0 is considered to be neither negative nor positive, we can actually get an additional number in the range above since we don't need two slots in the range to represent 0 (i.e., positive 0 and negative 0). With the way numbers are usually encoded, the extra number we squeeze out goes in the negative direction and we end up with the following range: [-128, 127].
Hence, if we're looking at using 8 bits of storage for a signed integer, then our base-10 range is [-2^(8-1), 2^(8-1) - 1] = [-2^7, 2^7 - 1]. If we want to use 16 bits to store (signed) integers, our range would be: [-2^15, 2^15 - 1] = [-32768, 32767]. And for 32 bits? We end up with [-2147483648, 2147483647]. Now, if we had an unsigned integer type, then our range would be [0, 2^32 - 1] = [0, 4294967295].
Aside: As a quick side note, suppose you are working in a 32-bit operating system. If you have done this before, then you know there is a limitation to the amount of memory that the 32-bit operating system can use. Memory spaces (bytes) are limited by their address number -> 32 bits. Every address is a byte and we have 4,294,967,296 bytes of addressable memory which translates to 4,294,967,296 bytes / 1024 kB = 4,194,304 kB, and this translates to 4,194,304 kB / 1024 MB = 4,096 MB, and this finally translates to 4,096 MB / 1024 GB = 4 GB.
How large an integer can be depends on how many bits are used to store the number. Some languages (e.g., Java, C, etc.) provide multiple distinct integer data types that use a fixed number of bits:
byte(signed 8-bit numbers; range:-128, ... , 127)short(signed 16-bit numbers; range:-32768, ..., 32767)int(signed 32-bit numbers; range:-2^31, ..., 2^31 - 1)long(signed 64-bit numbers; range:-2^63, ..., 2^63 - 1)
and more (for Java) ...
Python does not work this way. The int object uses a variable number of bits. As a number gets bigger, Python will simply increase the number of bits used to store that number. These accommodations are seamless to us. They are abstracted away and we do not have to deal with making such declarations. Since ints are actually objects, there is a further fixed overhead per integers. So, again, how can an integer become in Python? Theoretically, they are limited only by the amount of memory available. But of course large numbers will use more memory than smaller numbers.
At the most basic level, we can do something like the following to see how much space a "typical" integers takes up:
import sys
print(sys.getsizeof(0))
print(sys.getsizeof(1))
print(sys.getsizeof(-1))
We get back 24, 28, and 28. So at the very least an integer we use will take up 24 bytes of memory while the first nonzero integers take up 28 bytes of memory. It takes 4 bytes or 4 * 8 = 32 bits to store a small non-negative integer--we can see this due to the fact that 0 alone takes up 24 bytes in memory while, say, 1 takes up 28 bytes so 28 - 24 = 4 bytes. That's the difference in memory consumed. If we looked at 2^1000 or sys.getsizeof(2**1000), then we would get 160. So 160 bytes. How many bits did we use for the actual number? If we want to do that calculation we can do 160 minus the fixed overhead of 24 to get 136 bytes. We can multiply this by 8 to get the number of bits (1088). So this is how many bits we used to store the integer value of 2 ** 1000.
Integers - Operations
Let's now look at the different operations we can do with integers. Integers support all of the arithmetic operations we are used to: addition (+), subtraction (-), multiplication (*), division (/), and exponentiation (**). But what the resulting type of such an operation(s) is something we should ask ourselves:
int + int -> int
int - int -> int
int * int -> int
int ** int -> int
int / int -> float
The last observation above is worth remarking on. If we do something like 3 / 4, then it probably seems obvious a float would be returned as 0.75, but it may not be so obvious that 10 / 2 returns 5.0 (a float). So division always returns a float. This brings us to two more operations we have when dealing with integers, namely // or "div" (integer or floor division) and % or "mod" (modulo operator).

In general, the operators // and % always satisfy the following equation (n stands for numerator while d stands for denominator):
n = d * (n // d) + (n % d)
What exactly is floor division? We can define the floor of a (real) number as follows: The floor of a real number a is the largest (in the standard number order) integer less than or equal to a.
It is important to understand that // and % are defined in such a way that n = d * (n // d) + (n % d) is always true. Even when we are dealing with negative numbers. And that is where you have to be somewhat careful. You may get unexpected results if you are not paying close attention. Here are a few examples bundled into one to illustrate the differences:

Integers - Constructors and Bases
An integer is an object just like everything else in Python--it is an instance of the int class. Being a class, int provides multiple constructors. One constructor takes a single parameter and that parameter should be a numerical value (e.g., something like a decimal or a fraction or even an integer), and the second constructor takes a string and a second optional parameter.
As an example, we could call the constructor in the following ways:
a = int(10)
a = int(-10)
We usually do not call the int constructor in the ways mentioned above since, for example, a = 10 or a = -10 would be simpler alternatives. Other numerical datatypes are also supported in the argument of the int constructor:
a = int(10.9) # truncation: a -> 10
a = int(-10.9) # truncation: a -> -10
a = int(True) # a -> 1
a = int(False) # a -> 0
a = int(Decimal("10.9")) # truncation: a -> 10
The second constructor takes in a string (that can be parsed to a number) along with a second optional argument:
a = int("10") # a -> 10
But you can also specify the base of the number being passed as a string or not specify a base at all in which case the base defaults to 10 for the decimal system:
a = int("123") # a -> (123)_10
When used with a string, the int constructor takes an optional second parameter, base, where 2 <= base <= 36.
a = int("1010", 2) # a -> (10)_10
a = int("1010", base=2) # a -> (10)_10
a = int("A12F", base=16) # a -> (41263)_10
a = int("a12f", base=16) # a -> (41263)_10
a = int("534", base=8) # a -> (348)_10
a = int("A", base=11) # a -> (10)_10
a = int("B", base=11) # ValueError: invalid literal for int() with base 11: 'B'
Note how the keyword argument base is optional--it's good practice to include it for the sake of clarity. Also, if you use letters (depending on what base you are operating in), then the case does not matter.
In general, in terms of the bases that Python allows you to use, it uses 0-9 and a-z (so 10 characters plus 26 characters to get 36 characters in total). The following illustration may be somewhat helpful:
print(int("0", base=36)) # 0
print(int("1", base=36)) # 1
print(int("2", base=36)) # 2
print(int("3", base=36)) # 3
print(int("4", base=36)) # 4
print(int("5", base=36)) # 5
print(int("6", base=36)) # 6
print(int("7", base=36)) # 7
print(int("8", base=36)) # 8
print(int("9", base=36)) # 9
print(int("a", base=36)) # 10
print(int("b", base=36)) # 11
print(int("c", base=36)) # 12
print(int("d", base=36)) # 13
print(int("e", base=36)) # 14
print(int("f", base=36)) # 15
print(int("g", base=36)) # 16
print(int("h", base=36)) # 17
print(int("i", base=36)) # 18
print(int("j", base=36)) # 19
print(int("k", base=36)) # 20
print(int("l", base=36)) # 21
print(int("m", base=36)) # 22
print(int("n", base=36)) # 23
print(int("o", base=36)) # 24
print(int("p", base=36)) # 25
print(int("q", base=36)) # 26
print(int("r", base=36)) # 27
print(int("s", base=36)) # 28
print(int("t", base=36)) # 29
print(int("u", base=36)) # 30
print(int("v", base=36)) # 31
print(int("w", base=36)) # 32
print(int("x", base=36)) # 33
print(int("y", base=36)) # 34
print(int("z", base=36)) # 35
Hence, something like int("a12f", base=16) which we saw earlier is basically translated as follows:
(a12f)_16 = (a * 16^3) + (1 * 16^2) + (2 * 16^1) + (f * 16^0)
= (10 * 16^3)_10 + (1 * 16^2)_10 + (2 * 16^1)_10 + (15 * 16^0)_10
= (40960)_10 + (256)_10 + (32)_10 + (15)_10
= (41263)_10
Can we reverse the process described above? That is, can we easily change an integer from base 10 to another base? Yes. Python provides built-in functions to do this. For example, the bin(), oct(), and hex() built-in functions let us seamlessly convert decimals to base 2, 8, and 16, respectively:
a = bin(10) # a -> '0b1010' [base 2]
a = oct(10) # a -> '0o12' [base 8]
a = hex(10) # a -> '0xa' [base 16]
The prefixes in the strings help document the base of the number. You can even use these prefixes when using the int constructor: int('0xA', base=16) -> (10)_10. These prefixes are consistent with literal integers using a base prefix (no strings attached!):
a = 0b1010 # (1010)_2; a -> (10)_10
a = 0o12 # (12)_8; a -> (10)_10
a = 0xA # (A)_16; a -> (10)_10
So what about other bases? Can we take a base 10 number and get its representation in bases other than 2, 8, and/or 16 by using the built-in functions? Unfortunately, we need custom code for this. Python does not provide built-in functions to do this. We will need to do it ourselves or rely on a third-party library to help us do it.
Suppose n is a non-negative integer in base 10 (working with negatives is easy by symmetry), and we want to represent this base-10 integer in base b, the target base where 2 <= b <= 36. What does this mean? It means we want to find a string of base-b digits that represent that same number:
The div and mod equation we have seen previously will be useful here:
n = (n // b) * b + n % b
Let's see what happens if we try to represent (232)_10 in base 5: (?)_5? With n = 232 and b = 5, we have the following using the equation above:
232 = (232 // 5) * 5 + 232 % 5
= 46 * 5 + 2
= [46 * 5^1] + [2 * 5^0]
So we've obtained what seems to be the right-most digit in 2, but the other digit would be 46 and that makes no sense. We can iteratively apply our div and mod equation to pare things down effectively until "the other digit" is less than our base (e.g., we'd apply the equation now to n = 46 and b = 5):

We could leave things this way. After all, (232)_10 = (1412)_5. But we want to write our algorithm in as simple a way as possible. It's very nice that at each stage the "mod" number is part of our new base representation. But the last "div" instead of a mod is rather annoying. We could leave things like this and try to write some if statements perhaps, but there is a simpler way of going about this, and we will see it if we take things one step further:

This makes it possible to only use the "mod" numbers in our base-b representation and to stop our algorithm once the "div" value reaches 0.
Some pseudocode:
n = base-10 number (>= 0)
b = base (>= 2)
if b < 2 or n < 0: raise exception
if n == 0: return [0]
digits = []
while n > 0:
m = n % b
n = n // b
digits.insert(0, m)
Above, it is worth noting that for the assignment of m and n we could have just written m, n = n % b, n // b or m, n = divmod(n, b) since divmod(a,b) is the same as (a // b, a % b) for integers. Also, we could get a performance boost by not using insert for each iteration of the while loop--every insert results in our list having to be reindexed. It would be more performant to simply append to the list during every iteration and then reverse the list in place once the while loop has terminated. We will get to all of this soon. But note the results so far:
n = 232; b = 5; digits -> [1, 4, 1, 2]
n = 1485; b = 16; digits -> [5, 12, 13]
But 12 and 13 would be very confusing as symbols in base 16. It would be better for us to use some sort of encoding (e.g., a for 10, b for 11, etc., just as Python does internally when letting us specify the base when we use int). We simply need to decide what characters to use for the various digits in the base--we are not limited by anything. We could use emojis or special characters or whatever, but it is best to keep with A-Z or a-z to match how Python handles things on the complementary side. Whatever the case, we just need a map between the digits in our number to a character of our choice (i.e., we need to be able to map 10 to A, for example, and so on). Our choice of characters to represent the digits is our encoding map.
The following code is one approach to the problems we have described:
def from_base10(num, base):
if type(base).__name__ != 'int' or base < 2 or base > 36:
raise ValueError("base must be an integer with 2 <= base <= 36")
if type(num).__name__ != 'int':
raise TypeError("num must be an integer")
if num == 0: return "0"
digits_map = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
base_b_digits = []
while num > 0:
num, mod = divmod(num, base)
base_b_digits.append(mod)
base_b_digits.reverse()
encoding = "".join([digits_map[char] for char in base_b_digits])
return "-" + encoding if num < 0 else encoding
Rational numbers
Rational numbers are simply fractions of integer numbers. (e.g., 1/2, -22/7, etc.). Any real number with a finite number of digits after the decimal point is also a rational number (e.g., 0.45 -> 45/100, 0.123456789 -> 123456789/10^9, 8.3/4 -> 83/40, etc.).
It's useful to know about the Fraction class in Python. Rational numbers can be represented in Python using the Fraction class in the fractions module:
from fractions import Fraction
x = Fraction(3,4)
y = Fraction(22,7)
z = Fraction(6,10)
- Fractions are automatically reduced by the
Fractionclass:Fraction(6,10) -> Fraction(3,5). - A negative sign, if any, is always attached to the numerator:
Fraction(1,-4) -> Fraction(-1,4).
Let's look at some of the constructors:
# default
Fraction(numerator=0, denominator=1)
Fraction(other_fraction_object)
Fraction(float)
Fraction(decimal)
Fraction(string)
We have things like Fraction('10') -> Fraction(10, 1) or Fraction('0.125') -> Fraction(1, 8). More interesting, perhaps, is that you can actually introduce your fraction using a slash: Fraction('22/7') -> Fraction(22,7).
Standard arithmetic operators are supported (i.e., +, -, *, /) as well as other operators, and the result is a Fraction object too.
Fraction(2,3) * Fraction(1,2) -> Fraction(2,6) -> Fraction(1,3)
Fraction(2,3) + Fraction(1,2) -> Fraction(7, 6)
We can easily get the numerator and denominator of Fraction objects by using the numerator and denominator properties:
x = Fraction(22,7)
x.numerator # 22
x.denominator # 7
In terms of floats, float objects have finite precision. Any number we can store in a computer has finite precision. What this means is that any float object can be written as a fraction! We don't necessarily thing of them as a rational, but float objects cannot have an infinite decimal representation in our finite machine (i.e., computer). So any float object may also be represented as a fraction.
The upshot of this observation is we have things like the following:
Fraction(0.75) -> Fraction(3,4)
Fraction(1.375) -> Fraction(11,8)
Let's now work with numbers that we know are irrational (e.g., pi, square root of 2, etc.) and see how those are handled.
import math
from fractions import Fraction
x = Fraction(math.pi)
print(x) # Fraction(884279719003555, 281474976710656)
y = Fraction(math.sqrt(2)) # Fraction(6369051672525773, 4503599627370496)
print(y)
Even though pi and sqrt(2) are both irrational, internally these irrational numbers are represented as float objects. So what Python gives us is an approximation.
Warning: Converting a float to a Fraction has an important caveat. If we look at something like 1/8, then we need to realize this has an exact float representation--it is 0.125. So we get Fraction(0.125) -> Fraction(1,8). But something like 3/10, which is 0.3, does not have an exact float representation:
import math
from fractions import Fraction
x = Fraction(0.3)
print(x) # Fraction(5404319552844595, 18014398509481984)
Why do we get Fraction(5404319552844595, 18014398509481984) for Fraction(0.3) instead of Fraction(3,10)? This is because 0.3 isn't exactly 0.3 when it's stored as a float. It's slightly different. Let's see:
print(format(0.3, '.5f')) # 0.30000
print(format(0.3, '.10f')) # 0.3000000000
print(format(0.3, '.15f')) # 0.300000000000000
print(format(0.3, '.16f')) # 0.3000000000000000
print(format(0.3, '.17f')) # 0.29999999999999999
print(format(0.3, '.18f')) # 0.299999999999999989
print(format(0.3, '.19f')) # 0.2999999999999999889
print(format(0.3, '.20f')) # 0.29999999999999998890
print(format(0.3, '.25f')) # 0.2999999999999999888977698
print(format(0.3, '.30f')) # 0.299999999999999988897769753748
We'll get to the why of this soon when we talk about floats in detail.
Now, given a Fraction object, we can find an approximate equivalent fraction with a constrained denominator. What does this mean? We can use the limit_denominator instance method like so: limit_denominator(max_denominator=1000000). What this does is it finds the closest rational number (which could be precisely equal) with a denominator that does not exceed max_denominator:
import math
from fractions import Fraction
x = Fraction(math.pi)
print(x) # Fraction(884279719003555, 281474976710656)
print(x.limit_denominator(10)) # Fraction(22,7)
print(x.limit_denominator(100)) # Fraction(311,99)
print(x.limit_denominator(500)) # Fraction(355,113)
For other details, help(Fraction) is always useful.
Floats - Internal Representations
The float class is Python's default implementation for representing real numbers. The Python (CPython) float is implemented using the C double type which (usually!) implements the IEEE 754 double-precision binary float, also called binary64. Many languages use this implementation for storing float numbers.
The float uses a fixed number of bytes. They have a "fixed width". For integers, we saw they can "grow" in some sense (taking up more memory as they get larger), but floats are not like this. In particular, floats use 8 bytes or 64 bits. But in reality, Python has some memory overhead involving objects (and a float is an object in Python just like everything else). So when we create a float in Python, we're taking up more than just 64 bits--we're taking up 24 bytes. Hence, in general, any float we create in Python will take up 24 bytes. Of course, all of this is implementation dependent, but if you are using the CPython interpreter then you will likely be using the binary64 representation for floats.
These 64 bits are used up as follows for numbers:
| Item | Bit allocation | Description |
| sign | 1 bit | A 0 for positive and 1 for negative |
| exponent | 11 bits; range for exponents: [-1022, 1023] | 1.5E-5 -> 1.5 x 10^-5; the exponent is -5 |
| significant digits | 52 bits (the rest) | 15-17 significant (base-10) digits |
What are significant digits exactly? For simplicity: all digits except leading and trailing zeros.
1.2345 -> 5 significant digits
1234.5 -> 5 significant digits
12345000000 -> 5 significant digits
0.00012345 -> 5 significant digits
Note that for 12345000000 the 12345 are the significant digits while the number can also be represented as 12345E6 where 6 is the exponent. The same thing is true of 0.00012345 which can be represented as 12345E-8 where -8 is the exponent. But it still has only 5 significant digits. The leading or trailing zeros basically go into the exponent. The same would be true for, say, the number 12345E-50.
So how can we represent real numbers using a decimal or base-10 version? Numbers can be represented as base-10 integers and fractions. We already know everything we need to know about base-10 integers, but what do we really mean by the fraction part? Note the following:
0.75 -> 7/10 + 5/100 -> 7E-1 + 5E-2 (2 significant digits, 7 and 5)
0.256 -> 2/10 + 5/100 + 6/1000 -> 2E-1 + 5E-2 + 6E-3 (3 significant digits, 2, 5, and 6)
123.456 -> 1 * 100 + 2 * 10 + 3 * 1 + ...
In a more easily understood visual sense:
In general, we have the following:
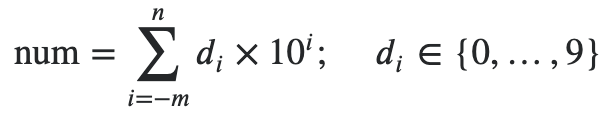
We're still missing the sign though. We will say the sign is some variable, say sign, where sign = 0 when num is non-negative and sign = 1 when num is negative. We can rewrite our formula above as follows:
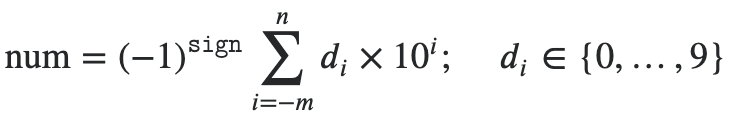
Hence, with num = 123.456, we have the following:

What we immediately notice when we do expansions like this is that some numbers cannot be represented using a finite number of terms. Of course, irrational numbers such as pi or sqrt(2) do not have a finite number of terms. But there are several examples of rational numbers not having any finite number of terms for our expansion (e.g., 1/3 is one such case).
Above, we saw how to represent float numbers in decimal form, and we saw how sometimes we can represent these numbers exactly like 0.75 with fraction expansion, but sometimes this is not possible (e.g., 1/3 equals 0.333333...). So now let's take a look at how we can represent these floating point numbers not in base 10 but in base 2 since that's what we have to work with when we're dealing with computers. We only have bits (0s and 1s).
Numbers in a computer are represented using bits (0s and 1s), not decimal digits. So instead of using powers of 10, we need to use powers of 2. All of our digits will be 0s and 1s whereas before they were allowed to be anywhere ranging from 0 to 9. Let's take a look at a binary float:
(0.11)_2 = 1 * 2^-1 + 1 * 2^-2 = 1/2 + 1/4 = 3/4 = (0.75)_10
Similarly,
(0.1101)_2 = 1/2 + 1/4 + 0/8 + 1/16 = 13/16 = (0.8125)_10
We can see the similarity to the general situation we had before for decimal numbers:
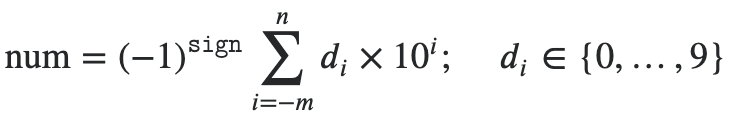
But now we're working in base 2 so we need to adjust things accordingly:
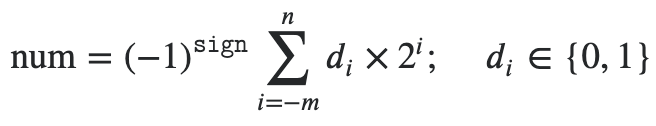
The same problem that occurs when trying to represent 1/3 using a decimal expansion also happens when trying to represent certain numbers using a binary expansion. For example, consider 0.1 or 1/10 in base 10. In base 10, we have no issue with this. 0.1 represents exactly the quantity 1/10. But this is not so in binary. Using binary freactions, this number does not have a finite representation:
(0.1)_10 = (0.0 0011 0011 0011 ...)_2
Hence, some numbers that have a finite decimal representation do not have a finite binary representation. The upshot of all this can be seen in the following summary:
(0.75)_10 = (0.11)_2 -> finite (exact float representation)
(0.8125)_10 = (0.1101)_2 -> finite (exact float representation)
(0.1)_10 = (0.0 0011 0011 0011 ...)_2 -> infinite (approximate float representation)
So we know in Python when we write 0.75 that is exactly what we are getting. It is exact. But when we write 0.1, we are not really getting this behind the scenes. We're getting something very close but not quite exact.
These kinds of small details may seem like "fussy business", but knowledge of these details could save you some headache in the future. For example:
a = 0.1 + 0.1 + 0.1
b = 0.3
a == b # False
print(format(a, '.25f')) # 0.3000000000000000444089210
print(format(b, '.25f')) # 0.2999999999999999888977698
Word to the wise: be careful with floats!
Floats - Equality testing
We will take a look at some of the problems that can arise when testing floats for equality. Previously, we saw problems that can arise based on how computers stored floats as binary expansions:
a = 0.1 + 0.1 + 0.1
b = 0.3
a == b # False
print(format(a, '.25f')) # 0.3000000000000000444089210
print(format(b, '.25f')) # 0.2999999999999999888977698
We saw that some decimal numbers with a finite representation (e.g., 0.1) cannot be represented with a finite binary representation. This can lead to some "weirdness" and bugs in our code (but not a Python bug!).
A naive attempt at a fix might involve rounding in some fashion. But it is no more possible to exactly represent round(0.1, 1) than 0.1 itself (i.e., rounding 0.1 to 1 decimal place is simply 0.1 itself):
round(0.1, 1) + round(0.1, 1) + round(0.1, 1) = round(0.3, 1) -> False
But it can be used to round the entirety of both sides of the equality comparison:
round(0.1 + 0.1 + 0.1, 5) == round(0.3, 5) -> True
This isn't very flexible though since this just involves round--and what exactly is rounding and how exactly does that work in Python? We may run into more issues (which we'll see soon).
Right now, to test for "equality" of two different floats, we could do the following methods:
- round both sides of the equality expression to a specified number of significant digits (e.g.,
round(a, 5) == round(b, 5)) - more generally, use an appropriate range (
epsilon) within which two numbers are deemed equal
The epsilon is essentially an error tolerance of sorts. It can be however large or small as we want. So a more general way of determining whether or not two floats a and b are equal may be as follows:
for some epsilon > 0, a = b if and only if |a - b| < epsilon
In practice, this definition may manifest itself as a method:
def is_equal(x, y, eps):
return math.abs(x-y) < eps
This can be tweaked by specifying that the difference btween the two numbers be a percentage of their size: the smaller the number, the smaller the tolerance; that is, are two numbers within x% of each other?
For either approach (i.e., the absolute value approach using epsilon or the percentage), there are non-trivial issues with using these simple tests (e.g., numbers very close to zero vs. numbers very far from zero)