Part 8 - Floating Point Data

Bit patterns are used to represent floating point numbers. More machine instructions are used to do floating point arithmetic.

Binary Fractions

Up until now all of the arithmetic we have done on the MIPS has been with integers, both signed (two's complement) and unsigned. This chapter starts the discussion of how floating point arithmetic is done on the MIPS.

Chapter Topics:

Positional notation with fractions
Converting fractions between base two and base ten
Fixed point representation
Limited precision of binary fractions (fixed point and floating point)
How "one tenth" cannot be expressed in binary
Dangerous program loops

Question 1

Is is possible to represent a negative integer with a positive number of bits?

Answer

Of course. Bit patterns can represent anything symbolic.

Bit patterns

The question is silly. There is nothing mysterious about representing signed numbers with bit patterns. Here is another silly question:

Is it possible to represent a fraction with a whole number of bits?

Of course. It is just a matter of picking a bit pattern for each fraction you wish to represent. There are several systematic ways to do this. This chapter discusses some of them.

Question 2

In the decimal value 12.6 what power of 10 is associated with:

The digit 1?
The digit 2?
The digit 6?

Answer

The digit 1? Answer: $10^1$
The digit 2? Answer: $10^0$
The digit 6? Answer: $10^{-1}$

Positional notation

This is just base 10 positional notation which you know about already. The decimal point is put between the $10^0$ position and the $10^{-1}$ position. Here is a longer example:

The notation 357.284 means 3 times 100, plus 5 times 10, plus 7 times 1, plus 2 times 0.1, plus 8 times 0.01, plus 4 times 0.001.

Question 3

Express 3/10 + 1/100 using positional notation.

__________

Answer

0.31

Base two positional notation

Positional notation can also be used with a base other than ten. Here is a number written using base two:

When a particular power of the base is not needed, the digit '0' is used for that position. If the base is two, the point '.' is called a binary point.

In general, the mark used to separate the fraction from the whole number is called a radix point. In many European nations, the radix point "," is used.

Question 4

What is 1×2^-1? (Express the answer in base ten notation).

____________

Answer

1×2^-1 = 1/(2¹) = 1/2 = 0.5

Base two to base ten

Recall that $X^{-n}$ means $1/X^n$ . So, $2^{-2}=1/4$ and $2^{-3}=1/8$ .

To convert an expression in base two notation to base ten notation, just do the arithmetic. Here is 100.101 convered from binary representation to decimal representation:

As you work, keep track of what parts of the expression are in base two and what parts are in base ten. In the above, the first row is in base two, the bottom row is in base ten, and the middle rows are polynomials.

Question 5

Write 0.11_2 as a base 10 expression.

__________

Answer

0.11₂ = 0×1 + 1×(0.5) + 1×(0.25) = 0.75

Include or exclude

In a binary representation a particular power of two is either included in the sum or not, since the digits are either "1" or "0".

A "1" bit in a position means to include the corresponding power of two in the sum. In converting representations, it is convenient to have a table.

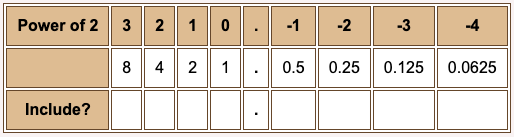
Question 6

What is 100.01_2 expressed in decimal?

__________

Answer

100.01_2 = 4.25

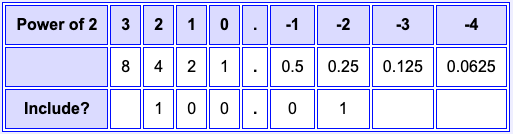
Fixed point notation

With paper-and-pencil arithmetic you can use as many digits or bits as are needed. But computers (usually) use a fixed number of bits for a particular data type. For example, MIPS integers are 32 bits. Can a fixed number of bits be used to express fractions?

Yes. Let us look briefly at an older method, not much used anymore. In the past, some electronic calculators and some computers used fixed point notation for expressing a fractional number. With fixed point notation, a number is expressed using a certain number of bits and the binary point is assumed to be permanently fixed at a certain position.

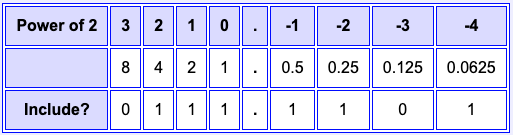
For example, let us say that fixed point numbers use eight bits and that the binary point is fixed between the middle two bits, like in the table. (In actual practice, the number of bits would be much more than eight.) Now to interpret an eight-bit expression, just copy the bits to the table.

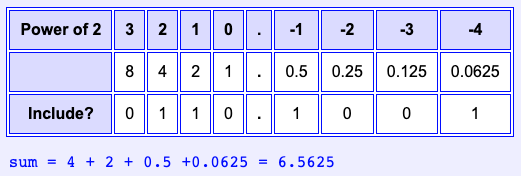
(Fill in the table by clicking the buttons. The powers of two above each 1-bit are included in the sum.)

Question 7

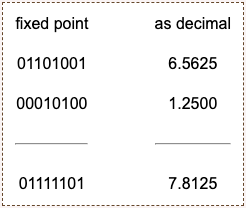
In this scheme, what does the bit pattern 01101001 represent in decimal?

Answer

Adding fixed point expressions

Here is another number: 00010100. This expression represents decimal 1.25.

Here is the familiar binary addition algorithm performed with the two bit patterns, and the usual decimal addition performed with their decimal equivalent.

Question 8

Of course, the question is, does the sum of the fixed point expressions (01111101) represent the sum of the decimal expressions (7.8125)?

You can satisfy your burning curiosity by adding up the included decimals in the table.

Answer

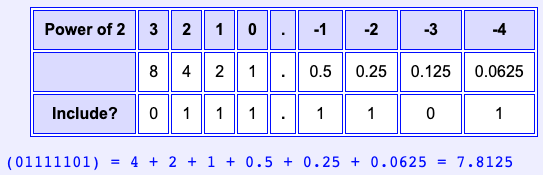
Binary addition algorithm works

The binary addition algorithm works for our eight-bit fixed point notation! In early computers and calculators this enabled the same electronic circuits to be used for integer arithmetic (both signed and unsigned) and for fixed point arithmetic. This looks very promising.

However, fixed point is not as useful as the floating point representation which has replaced it. Floating point will be discussed in the next chapter.

Question 9

How many values can be represented using our 8-bit fixed point representation?

Answer

$2^8 = 256$

Limited precision

This is an easy question. If N bits are used, then only 2^N things can be represented, no matter what type of things they are. Eight bits can represent 256 positive integers (unsigned binary), 256 positive and negative integers (two's complement), 256 fractional numbers (our fixed point method), and so on. Here is a number line showing the 256 values that can be represented with this fixed notation:

The smallest value is zero (00000000). The largest value is 15.9375 (11111111). The smallest non-zero value is 0.0625. Every represented value is a multiple of 0.0625.

Another way to think of fixed point notation is that the eight bits represent an integer from 0 to 255. The integer is a multiplier of the value 0.0625.

The range between any two integers is divided into 16 numbers (because 16*0.0625 = 1.0). This is not very many divisions. There are big gaps between represented numbers.

Important points: With our version of 8-bit fixed point, the only numbers that can be represented lie in the range zero to 15.9375. This is called a limit in range. Also, only a few real numbers within that range can be represented. This is called a limit in precision.

All schemes for representing real numbers with bit patterns have limited range and limited precision. This is true for the usual floating point representations of computers. No matter how many bits are used, there are limits on the range and precision.

Question 10

(Calculus Review:) How many real numbers lie between 0.0 and 0.0625?

Answer

An infinite number.

Infinitely many missing numbers

The limited precision of fixed point (and floating point) expressions is a problem for programmers. Even with 64-bit double precision floating point (such as Java data type double) precision is limited. Only 2^64 numbers can be represented. This is a lot, but between any two numbers that are represented there are an infinite number of real numbers that are not represented!

(If your calculus is a little vague, don't worry. Just think about the nearly infinite number of atoms between any two marks on even the most precise ruler.)

Question 11

How many digits does the value pi have?

Answer

An infinite number of digits (or bits).

Shifting left one bit

Let us return to paper-and-pencil positional notation. Here is a binary expression:

0001.0100 = 1.25_10

Here is the same pattern, shifted left by one bit:

0010.1000 = 2.50_10

Question 12

What does shifting left by one bit do?

Answer

Multiplies by two. This is the same as with unsigned integers. Also, shifting one bit right is equivalent to division by two.

Converting representatives from decimal to binary

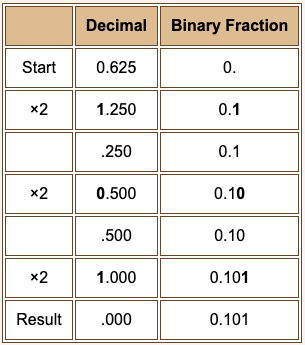
Often you need to convert a decimal expression like 7.625 into a binary expression. To do this, first convert the whole number (7 in this case) to binary (111 in this case), append a binary point, and convert the decimal fraction to binary.

To convert a decimal fraction to Base 2: Repeatedly multiply the decimal fraction by two. After each multiplication, a bit moves into the one's place (the place just left of the binary point). Copy that bit to the right of the binary fraction, then erase it from the decimal fraction.

Stop when the decimal fraction is zero. (If this never happens, stop when you have enough bits in the binary fraction.)

For our example: 7.625 is 111.101₂. In this case the conversion stops when the decimal fraction changes to zero. This does not always happen.

Question 13

(Thought Question:) Why will no other digit but 0 or 1 move into the one's place? (Hint: consider the biggest possible decimal fraction).

Answer

You might fear that a '2' or higher digit might move into the one's place. Try this: multiply the biggest decimal fraction 0.99999... by two. This yields 1.99999... Even with this fraction a '1' moves into the one's place.

Practice

Here is an table set up to convert 0.75 to binary. Fill in the table by typing numbers in the boxes. Or, do the work with pencil-and-paper.

Question 14

Perform the conversation.

Answer

Non-terminating result

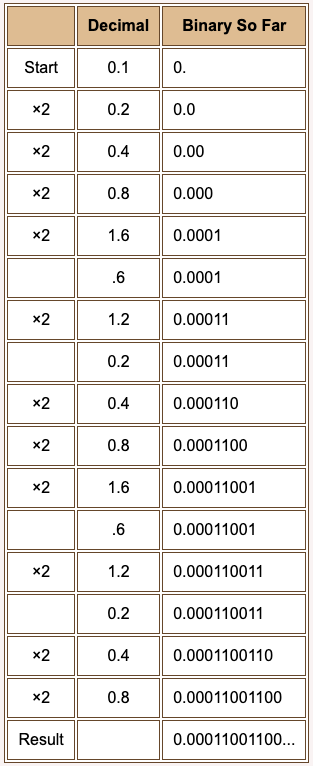
At right the algorithm is used to convert 0.1_10 to binary. (The "erase" steps are not shown when a 0 is copied to the "binary so far" column.)

The algorithm does not end. After it has started up, the same pattern 0.2, 0.4, 0.8, 1.6, 0.6, 1.2, 0.2 repeats endlessly. The pattern 0011 is appended to the growing binary fraction for each repetition.

Unexpected Fact: The value "one tenth" cannot be represented precisely using a binary fraction.

This is true in the base two positional notation used here, and also in floating point representation used in programming languages. This is sometimes an important consideration when high accuracy is needed.

Question 15

Can "one third" be represented accurately in decimal?

Answer

No. Its representation continues indefinitely: 0.3333333....

The problem with "one tenth" is not a special flaw of binary. With all bases there are fractions that cannot be represented exactly.

Dangerous code

Here is a program fragment in Java. (It could also be in C or C++). Is there something in this program that you should worry about?

float x;

for ( x = 0.0; x != 10.0; x += 0.1 )
{
  System.out.println("Crimson and Clover");
}

Question 16

How many times will "Crimson and Clover" be printed?

Answer

Over and over.

Hidden infinite loop

If we were using base 10 arithmetic, 0.1 would be added to x 100 times until x reached exactly 10.0. But the program uses base-two floating point which does not represent 0.1 exactly. The variable x might not hit 10.0 exactly and the program would then loop indefinitely.

float x;

for ( x = 0.0; x != 10.0; x += 0.1 )
{
  System.out.println("Crimson and Clover");
}

It is not just binary fixed point representation that cannot represent one tenth precisely. The usual floating point of programming languages has the same problem.

Smart compilers look out for this problem, and may fix it, so this loop might actually work as intended. But is not wise to use it.

Question 17

Fix the code.

float x;

for ( x = 0.0; x != 10.0; x += 0.1 )
{
  System.out.println("Crimson and Clover");
}

Answer

See below.

Count with integers

If the purpose of the program fragment is to loop 100 times, then a counting loop using an integer variable should be used. Here is the best fix:

int x;

for ( x = 0; x < 100; x++ )
{
  System.out.println("Crimson and Clover");
}

(It is conventional to write a counting loop this way, even though testing for an "exact hit" with x != 100 is logically equivalent.) Here is a poor solution:

float x;

for ( x = 0.0; x < 10.0; x += 0.1 )
{
  System.out.println("Crimson and Clover");
}

This will probably work as intended, but there is a risk it will loop 101 times.

Question 18

Say that you need 100 values, 0.0, 0.1, up to 9.9? Can an integer-controlled counting loop be used?

Answer

Yes.

Calculate each float

Use the for-loop structure to correctly and safely count. Calculate a new value of the floating point variable each time.

double x;
int    j;

for ( j = 0; j < 100; j++ )
{
  x = j/10.0;
  
  // do something with x
}

Almost always, floating point work should be done with double precision, as above. An even more accurate version of the loop is:

double x;
int    j;

for ( j = 0; j < 160; j++ )
{
  x = j/16.0;
  
  // do something with x
}

This is better because (1/16) is accurately represented in binary.

Question 19

Is floating point representation (as used in computers) the same as the base two notation discussed in this chapter?

Answer

No. They are related, but floating point is more sophisticated. The next chapter discusses it.

Chapter quiz A

Question 1

In the decimal fraction 12.345 what power of 10 is the digit 5 associated with?

(A) -3
(B) -2
(C) -1
(D) 1

Answer

Question 2

In the binary fraction 10.001 what power of 2 is the rightmost bit associated with?

(A) -3
(B) -2
(C) 1
(D) -1

Answer

Question 3

Express 1 + 4/10 + 3/100 using base 10 positional notation.

(A) 1.043
(B) 143.00
(C) 1.43
(D) 0.143

Answer

Question 4

Express 1 + 1/2 + 0/4+ 1/8 using base 2 positional notation.

(A) 1.11
(B) 1.011
(C) 11.1
(D) 1.101

Answer

Question 5

What is 2^-1 ? (Express the answer in base 10)

(A) 1/2
(B) 1/4
(C) 1/8
(D) 2

Answer

Question 6

Write 1.01₂ as a base 10 expression.

(A) 1.125
(B) 1.25
(C) 1.5
(D) 1.625

Answer

Question 7

Say that the following is a four bit binary fixed-point expression and that the point is fixed between the middle two bits.

What value does it represent? (Write the answer in decimal.)

(A) 10.75
(B) 2.3
(C) 2.75
(D) 1.625

Answer

Question 8

Here is another four bit binary fixed-point expression with the point is fixed between the middle two bits.

What value does it represent? (Write the answer in decimal.)

(A) 1.25
(B) 2.2
(C) 1.625
(D) 0.25

Answer

Question 9

Perform the following addition of fixed-point binary operands using the Binary Addition Algorithm. Assume that the binary point is in the middle. What value does the sum represent?

1011
0001
----

(A) 1100 represents 12₁₀
(B) 0110 represents 1.5₁₀
(C) 1100 represents 3.5₁₀
(D) 1100 represents 3₁₀

Answer

Question 10

A method that uses only four bits can represent only 16 values. This is described as a limit on its ________.

(A) Accuracy
(B) Precision
(C) Magnitude
(D) Resolution

Answer

Question 11

Which one of the following statments is true?

(A) Computer arithmetic is so precise that if the input values are correct, all calculations will be accurate.
(B) Computer arithmetic is always much more precise than an ordinary electronic calculator.
(C) Even when using double precision floating point it is easy for errors in a calculation to accumulate until the result is meaningless.
(D) Sixtyfour bits of precision is more than anyone could ever want.

Answer

Question 12

The number 0.625 is here represented as a decimal fraction. Multiply it by two. Copy the one's place digit of the result to the beginning of a binary fraction. What is the beginning the binary fraction that represents the number?

(A) 0.1
(B) 0.0
(C) 1.1
(D) 2.0

Answer

Question 13

After multiplying the number by two and dropping the digit to the right of the decimal point you are left with 0.25. Multiply this by two and copy the one's place digit of the result to the binary fraction. What is the binary fraction so far?

(A) 0.11
(B) 0.10
(C) 1.01
(D) 0.01

Answer

Question 14

The number you are working on now looks like: 0.5. Repeat the above process to complete the binary fraction. The number 0.625 represented as a binary fraction is:

(A) 0.111
(B) 1.011
(C) 0.110
(D) 0.101

Answer

Question 15

Represent the decimal fraction 0.375 as a binary fraction.

(A) 0.11
(B) 0.111
(C) 0.011
(D) 0.001

Answer

Question 16

Which of the following binary fractions is an approximation to the decimal fraction 0.8?

(A) 0.11001
(B) 0.10101
(C) 0.11010
(D) 0.0111

Answer

Question 17

If you know how many times a loop should execute, the loop control variable should be:

(A) float
(B) double
(C) boolean
(D) int

Answer

Question 18

Say that you have a while loop that uses a conditional expression that involves floating point variables. Which one of the following comparison operators should not be used in the conditional expression?

(A) ==
(B) >
(C) <
(D) <=

Answer

Question 19

Which one of the following decimal fractions cannot be represented accurately using a binary fraction?

(A) 0.5
(B) 0.0
(C) 0.1
(D) 0.125

Answer

Question 20

Most programs that do floating point calculations should use variables of what type?

(A) double
(B) float
(C) single
(D) real

Answer

Chapter quiz B

Instructions: For each question, choose the single best answer. Make your choice by clicking on its button. You can change your answers at any time. When the quiz is graded, the correct answers will appear in the box after each question.

Question 1

Express 5 + 0/2 + 1/4 + 0/8 + 1/16 using base 2 positional notation.

(A) 5.0110
(B) 101.0101
(C) 101.101
(D) 111.0101

Answer

Question 2

Express 110.1001₂ as a sum of decimal integers and fractions

(A) 4 + 2 + 1/2 + 1/16
(B) 4 + 2 + 1/2 + 1/32
(C) 4 + 2 + 1/4 + 1/16
(D) 6 + 3/16

Answer

Question 3

Express 1001.1011₂ as a sum of a single decimal integer and a single decimal fraction.

(A) 10 + 11/2
(B) 9 + 11/8
(C) 9 + 11/16
(D) This cannot be done.

Answer

Question 4

Express the decimal value 7 and 3/8 in binary.

(A) 101.11
(B) 111.11
(C) 111.011
(D) 111.001

Answer

Question 5

Express the decimal value 0.6250 as binary.

(A) 0.1010
(B) 0.0110
(C) 0.1100
(D) 0.1001

Answer

Question 6

Express 0.3125 as binary

(A) 0.1001
(B) 0.1100
(C) 0.1011
(D) 0.0101

Answer

Question 7

Express the binary 1.1001 as a decimal fraction.

(A) 1.5625
(B) 1.7500
(C) 0.6252
(D) 1.8750

Answer

Question 8

Express the decimal value 0.73 as an approximation in binary

(A) 0.11010
(B) 0.10111
(C) 0.01101
(D) 0.10010

Answer

Question 9

Express the decimal 0.5940 in a binary approximation.

(A) 0.10010
(B) 0.10101
(C) 0.011111
(D) 0.10011

Answer

Question 10

Express the decimal 0.34375 in binary

(A) 0.01011
(B) 0.01101
(C) 0.01010
(D) 0.11011

Answer

IEEE 754 Floating Point

This chapter is about the IEEE 754 floating point standard. This is a standard for the floating point numbers that are used in nearly all computers and programming languages since 1985. Java floating point (on its virtual processor) and MIPS floating point (on real hardware) conform to this standard.

Chapter Topics:

Why use floating point?
History of floating point
Scientific notation
Precision of floating point
IEEE 754 floating point standard
Converting to floating point notation

Question 1

(Review:) Is it absolutely essential that a processor support floating point data?

Answer

No. All that a processor needs is a small set of basic instructions. Everything else can be built up from them.

Why floating point?

Floating point representation makes numerical computation much easier. You could write all your programs using integers or fixed-point representations, but this is tedious and error-prone. For example, you could write a program with the understanding that all integers in the program are 100 times bigger than the number they represent. The integer 2345, for example, would represent the number 23.45. As long as you are consistent, everything works.

This is actually the same as using fixed point notation. In fixed point binary notation the binary point is assumed to lie between two of the bits. This is the same as an understanding that the integer the bits represent should be divided by a particular power of two.

But it is very hard to stay consistent. A programmer must remember where the decimal (or binary) point "really is" in each number. Sometimes one program needs to deal with several different ranges of numbers. Consider a program that must deal with both the measurements that describe the dimensions on a silicon chip (say 0.000000010 to 0.000010000 meters) and also the speed of electrical signals, 100000000.0 to 300000000.0 meters/second. It is hard to find a place to fix the decimal point so that all these values can be represented.

Notice that in writing those numbers (0.000000010, 0.000010000, 100000000.0, 300000000.0) I was able to put the decimal point where it was needed in each number.

Question 2

(Take a guess: ) When the decimal point moves to where it is needed in an expression, the decimal point is said to ____________.

Answer

Float.

Floating point

The essential idea of floating point representation is that a fixed number of bits are used (usually 32 or 64) and that the binary point "floats" to where it is needed in those bits. Of course, the computer only holds bit patterns. Some of the bits of a floating point representation must be used to say where the binary point lies.

Floating point expressions can represent numbers that are very small and numbers that are very large. When a floating point calculation is performed, the binary point floats to the correct position in the result. The programmer does not need to explicitly keep track of it.

Question 3

Is floating point an old or a modern idea?

Answer

Old.

Early floating point

The first digital computer (according to some) the Z3, built by Konrad Zuse in 1941 used floating point representation. This computer had a clock speed of five to ten Hertz and a memory of 64 words of 22 bits! (The earlier Z1 machine also used floating point, but was not quite programmable enough to be considered a computer.)

Early computers were built to do engineering and scientific calculation so it is no surprise that the invention of floating point happened at the same time. In later years it was realized that computers are very useful things, and not just for calculation. Often floating point was not supported.

Many early minicomputers and microprocessors did not directly support floating point in hardware. For example, Intel processor chips before the 80486 did not directly support floating point. A floating point operation in a program (written in C, say) was compiled into a sequence of bit-manipulation instructions that did the required operations. Computers used for graphics or engineering calculation often had an additional chip that performed floating point operations in hardware.

MIPS processors are very strong on floating point, and have supported the IEEE standard from their (and its) beginning. MIPS chips are often used in high-end engineering and graphics workstations and are famous for their fast floating point.

Question 4

(Not very hard thought question:) Do you imagine that in (say) 1975 that the floating point methods used on IBM mainframes were the same as on DEC minicomputers?

Answer

No.

Floating point compatibility

Up until 1985 each hardware manufacturer had its own type of floating point. Worse, different machines from the same manufacturer might have different types of floating point! And when floating point was not supported in the hardware, the different compilers emulated different floating point types.

The situation was awful. Consider a magnetic tape full of data written by an IBM mainframe. Now the tape must be read by a DEC minicomputer. Assume that the bits on the tape can be read correctly. But DEC uses a different type of floating point than IBM. Interpreting those bits is hard! This is a common problem with "legacy data." NASA (the USA National Aeronautical and Space Administration) has warehouses full of tapes from various space missions written in many different formats. Much of this data is turning to dust for lack of programs that can read it.

Question 5

Should the same numerical calculation, performed on two different computers, give the same result on each?

Answer

Yes. But before a floating point standard this was sometimes not true.

Scientific notation

To address this problem the IEEE (Institute of Electrical and Electronics Engineers) created a standard for floating point. This is the IEEE 754 standard, released in 1985 after many years of development. All hardware and software since then follow this standard (many processors also support older standards as well).

The idea of floating point comes from scientific notation for numbers. You have probably seen this before (and may already be shuddering). Here is a number in scientific notation:

The mantissa always has a decimal point after the first digit. The above expression means:

1.38502 × 1000 = 1385.02

The decimal point "floats" to where it belongs. In effect, the mantissa gives the digits and the exponent says where the decimal point should go.

Question 6

Write the following in scientific notation: 243.92

Answer

243.92 = 2.4392 × 10⁰²

Negative exponents

The exponent shows by what power of 10 to multiply the mantissa, or (the same thing) how far to float the decimal point.

10⁺ⁿ means move the decimal point `n` places right.10^-n means move the decimal point `n` places left.

Question 7

Write 0.000456 in scientific notation.

Answer

0.000456 = 4.56 × 10^-4

There must be only one digit to the left of the decimal place, so an answer like 45.6 × 10^-5 is not in the correct format.

Negative values

The notation for a negative number has a negative sign in front of the first digit:

-1.38502 × 10^(03) = -(1.38502 × 10^(03)) = -1385.02

The notation for a small negative number has two negative signs: one to negate the entire number and one (in the exponent) to shift the decimal point left:

-1.38502 × 10^(-3) = -(1.38502 × 10^(-3)) = -0.00138502

Question 8

Match the numbers in column I with the scientific notation in column II.

Answer

Click!

e

Writing the multiplication symbol (×) and the superscript exponent is tedious, and not suitable for programs. A slightly altered notation is used in computer programs and in input and output text:

1.38502 × 10⁺⁰³ = 1.38502e+03
1.38502 × 10^-03 = 1.38502e-03
-1.38502 × 10⁺⁰³ = -1.38502e+03
-1.38502 × 10^-03 = -1.38502e-03

Caution: For SPIM, only a small "e" is allowed in floating point constants. (Some software systems, such as Java, allow both upper and lower case e's).

Question 9

How many digits are in each of the above expressions? How many digits are in the mantissa? How many in the exponent?

Answer

How many digits are in each of the above expressions? 8

How many digits are in the mantissa? 6

How many in the exponent? 2

Fixed number of digits

The question and its answer is getting close to the idea of floating point. Each expression has eight digits. Two of the digits are used to "float" the decimal point. The remaining six show the digits of the number.

The number of digits in the mantissa is called the precision of the floating point number. When we start talking about binary floating point, the precision will be the number of bits in the mantissa. With a 32-bit single-precision floating point value the mantissa is 24 bits, so single precision floats have 24 bits of precision.

Caution: sometimes in casual speech people say that single precision values have 32 bits of precision, but this is not actually correct.

Another Caution: the mantissa uses 23 bits to represent its 24 bits of precision. This trick will be discussed shortly.

Question 10

How many possible mantissas can be represented in single precision?

Answer

A mantissa has 23 bits so there are 2^23 patterns possible.

IEEE 754 Floating Point

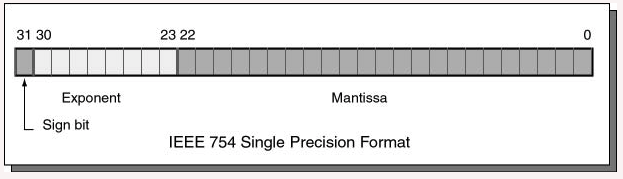
An IEEE 754 single-precision floating point value is 32 bits long. The bits are divided into fixed-sized fields as follows:

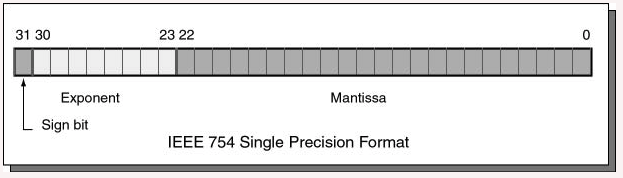
Bits 0 through 22 are for the mantissa; bits 23 through 30 are for the exponent; and bit 31 is the sign bit. The mantissa and exponent fields work like the similar parts in scientific notation (details follow). The sign bit gives the sign of the entire expression: a 0 bit means positive and a 1 bit means negative.

Question 11

You have seen the MIPS instruction bltz which branches if the 32-bit integer in a register is less than zero (negative). It does this by looking at bit 31 of the two's complement integer and branching if it is set.

Does this instruction work with single precision values?

Answer

Yes. The sign bit of 32-bit integers and of 32-bit floats is set (to one) when the value is negative and clear (to zero) when the value is positive or zero.

More on Ms. Mantissa

The mantissa represents a number in 24-bit base two positional notation that looks like this:

1.xxxxxxxxxxxxxxxxxxxxxxx     (x = 0 or 1; there are 23 x's)

Very tricky: The mantissa represents the 23-bit binary fraction part of a 24-bit number that starts with a "1". The 2^0 place (the one's place) is presumed to contain a 1 and is not present in the mantissa. This trick gives us 24 bits of precision with only 23 bits.

For example, the binary number 1.11110000101101101010001 is represented as 11110000101101101010001.

Question 12

If you had a daughter would you name her Mantissa?

Answer

What a sweet name!

How the mantissa works

Since leading zeros of a binary number can be dropped, it is safe to not actually include the first 1. There will always be one, so there is no need to show it.

The exponent is adjusted so that the most significant 1 is in the one's place of the mantissa. Then that 1-bit is dropped. For example: say that you wish to represent 00011.00101101 as a float.

Drop the leading zeros:
```
11.00101101
```
Now there is a leading one.
Move the binary point so that the leading one is in the one's place (the exponent shows the move):
```
1.100101101 × 2^1
```
Drop the leading one:
```
100101101 × 2^1
```
Add zero bits on the right so that there are 23 bits in total:
```
10010110100000000000000 × 2^1
```
Result: the mantissa is: 10010110100000000000000

Question 13

Is the mantissa always zero or positive?

Answer

Yes. (The sign bit is not part of the mantissa).

Practice

You must be eager to try this yourself!! Here is an opportunity. The decimal value 7.46875 written in base two positional notation is 00111.01111. What is the mantissa of this number?

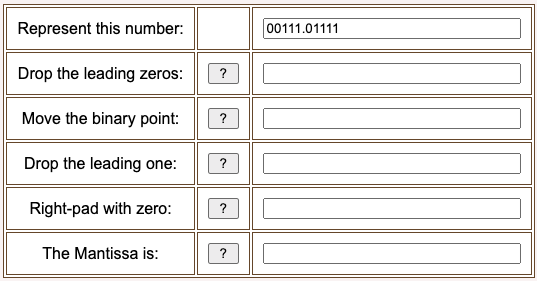
Result:

Question 14

(Review:) What part of the single precision float represents the shifted binary point?

Answer

The exponent.

The exponent

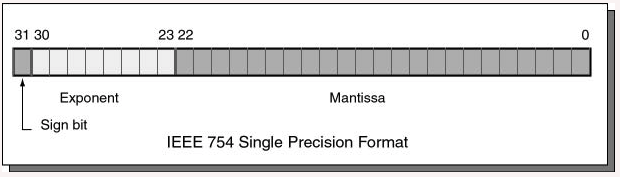
The eight bits 23 through 30 contain the exponent. The exponent is an integer, but may be negative, zero, or positive. You might guess that an 8-bit two's complement integer would work perfectly for this, but a different type of notation is used.

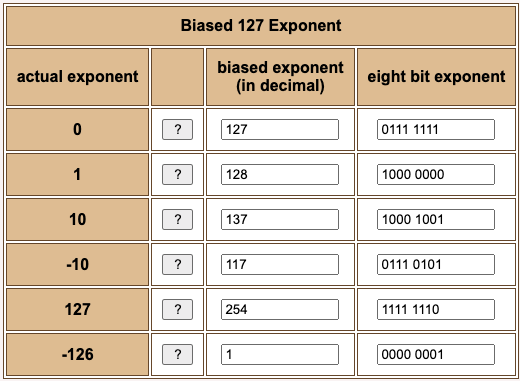
The exponent is expressed using a biased integer. The true exponent is added to +127₁₀ resulting in an unsigned binary integer. The biased integer is encoded using 8-bit unsigned binary.

A biased exponent of +127 represents the actual exponent 0.
A biased exponent of +128 represents the actual exponent 1.
A biased exponent of +126 represents the actual exponent -1.

Exceptions: (1) A floating point value of 0.0 is represented with a mantissa of 23 zero bits and an exponent of 8 zero bits. It is not legal to have an exponent of zero with a non-zero mantissa. (2) The exponent 255₁₀ (1111 1111) is used to signal various problems, such as division by zero.

Question 15

What is the mantissa when the entire float is zero?

Answer

Zero.

Exponent practice

The sign bit is zero when the number is zero. A floating point zero consists of 32 zero bits. The MIPS instructions that test for integer zero can test for floating point zero.

IEEE floating point also represents "negative zero", where the sign bit is set (to one), and all other bits are zero. In mathematics, negative zero is the same as zero. But floating point calculations sometimes give different results for "positive zero" and "negative zero". This is an advanced topic; for these chapters assume that zero is represented with 32 zero bits.

In the following chart, first convert the actual exponent to a biased exponent, then write the biased exponent as an eight bit binary.

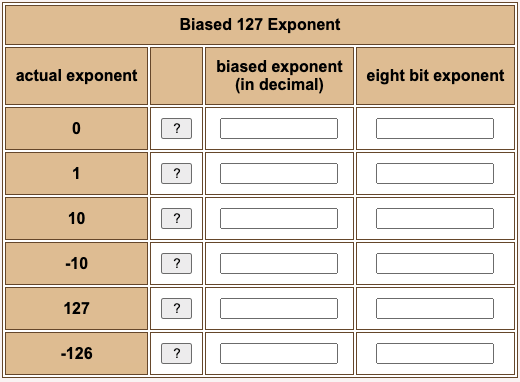
Result:

Question 16

How is the exponent -127 represented?

Answer

It is not represented. (Remember, the biased exponent 0000 0000 is used for the value zero).

Float formula

Here is a formula that summarizes the past several pages. In it, s is the sign bit (0 or 1), M is the mantissa (000...000 to 111...111) and E is the biased exponent.

value = (-1)^s × 1.M × 2^E-127

To convert a paper-and-pencil number into IEEE floating point, fill in each piece of the picture. Let us represent 1.0 as a 32-bit IEEE 754 float.

Question 17

What is the sign bit of 1.0?
What is the mantissa of 1.0? (Hint: remember the assumed "1." preceding the mantissa)
What is the actual exponent of 1.0?
What is the biased exponent of 1.0? (Hint: add the actual exponent to 127)

Answer

What is the sign bit of 1.0? 0 (for positive)
What is the mantissa of 1.0? 000 0000 0000 0000 0000 0000
What is the actual exponent of 1.0? 0
What is the biased exponent of 1.0? 127_10 = 0111 11112

1.0

Fitting each of these pieces into their proper fields gives us the full 32 bits:

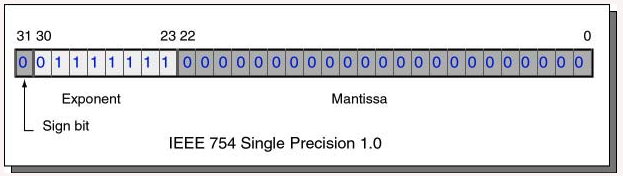
If the bit pattern is written in hexadecimal it is 0x3F800000. To check that this is correct, use SPIM. Write a program that declares a floating point 1.0, then run SPIM.

## Program to represent 1.0
        .text
        .globl  main
main:
        .data
val:    .float    1.0
## End of file

Question 18

When you load this program in SPIM, where will the 1.0 be?

Answer

The 0x3F800000 will be in the DATA section in the 32 bits starting at address 0x10010000.

SPIM data

Of course, to the memory system a 32-bit floating point value is just another 32 bit pattern. Here is part of SPIM's display showing this:

Question 19

(Review:) Can -0.1 be represented precisely as a 32-bit float?

Answer

No. Remember from the last chapter that 0.1 can't be represented precisely in binary. Using floating point representation does not change anything. It does not matter that the number is negative.

-0.1

But let us proceed to see how -0.1 is (imprecisely) represented.

The sign bit of -0.1 is 1 (for negative).
The binary fraction for 0.1 (from the previous chapter is)
```
0.0001100110011001100110011001100...
```
The mantissa of 0.1 is:
- Shift the leading bit into the one's place: 1.100110011001100110011001100...
- The shift was 4 places left, for an exponent of -4
- Drop the one bit in the one's place: .100110011001100110011001100...
- Retain 23 bits: 100 1100 1100 1100 1100 1100
The actual exponent is -4
The biased exponent is 127-4 = 123 = 0111 1011

Question 20

Here are the bits written out:

Write out the bit pattern as hexadecimal.

Answer

On SPIM, a constant of -0.1 is represented as 0xBDCCCCCD because the value is rounded up one bit to form the "D" at the end.

Chapter quiz

Question 1

What does the "IEEE" (as in "IEEE 754 Floating Point") stand for?

(A) Industry Electrical Evaluation Enterprise
(B) International Enterprise for Electronics Education
(C) Institute of Electrical and Electronics Engineers
(D) Interstate Engineering and Electrification Effort

Answer

Question 2

How is 1.234 × 10³ normally written?

(A) .0001234
(B) 12.34
(C) 123.4
(D) 1234

Answer

Question 3

Write 0.0345 in scientific notation

(A) 3.45 × 10^-2
(B) 3.45 × 10^-3
(C) 3.45 × 10⁺³
(D) -3.45 × 10²

Answer

Question 4

Which part of 1.2345 × 10²³ is the mantissa?

(A) 23
(B) .2345
(C) 10
(D) 1.2345

Answer

Question 5

Write 0.00623 in scientific notation.

(A) 6.23 × 10^-3
(B) .623 × 10^-3
(C) 6.23 × -10³
(D) 6.23 × -10^-3

Answer

Question 6

Which expression of the following is how 1.223 × 10^-5 would appear in a source file.

(A) 1.223e05
(B) 1.223EE5
(C) 1.223e-5
(D) 1.223-5
(E) 1.223E^5

Answer

Question 7

A 32-bit IEEE 754 float consists of three fields: sign bit, biased exponent, and mantissa. How many bits are in each one?

(A) 1, 12, 19
(B) 2, 15, 15
(C) 1, 8, and 23
(D) 1, 4, 27

Answer

Question 8

Here is a formula that says how the three fields combine to represent a number: value = (-1)^s × 1.M × 2^E-127

What biased exponent would be used to represent 2²?

(A) 3₁₀, represented as 0000 0011
(B) -124₁₀, represented as 1000 0100
(C) 128₁₀, represented as 1000 0000
(D) 129₁₀, represented as 1000 0001

Answer

Question 9

Say that you wish to represent 001.0011₂ as a IEEE 754 float. What is the 23-bit mantissa?

(A) 100110000000000000000000
(B) 001100000000000000000000
(C) 00110000000000000000000
(D) 11000000000000000000000

Answer

Question 10

Say that you wish to represent 010.1011011₂ as a IEEE 754 float. What is the 23-bit mantissa?

(A) 01011011000000000000000
(B) 101011011000000000000000
(C) 0101101100000000000000
(D) 01010110110000000000000

Answer

Floating Point Arithmetic on MIPS

MIPS chips use the IEEE 754 floating point standard, both the 32 bit and the 64 bit versions. However these notes cover only the 32 bit instructions. The 64 bit versions are similar.

Chapter Topics:

Floating point registers
Loading and storing floating point registers
Single and (some) double precision arithmetic
Data movement instructions
Reading and writing floating point

SPIM Settings for this chapter: set SPIM to allow pseudoinstructions, disable branch delays, and disable load delays.

Question 1

The 64 bit (double precision) floating point numbers are better than 32 bit (single precision). But how are they better?

Increased Precision?
Greater Range of values covered?
Both?

Answer

Both. Double precision numbers have more bits for the exponent (so the range of values is increased) and more bits in the mantissa (so the precision is increased).

MIPS floating point

Floating point on MIPS was originally done in a separate chip called coprocessor 1 also called the FPA (Floating Point Accelerator). Modern MIPS chips include floating point operations on the main processor chip. But the instructions sometimes act as if there were still a separate chip.

MIPS has 32 single precision (32 bit) floating point registers.

The registers are named $f0 — $f31
$f0 is not special (it can hold any bit pattern, not just zero).
Single precision floating point load, store, arithmetic, and other instructions work with these registers.
Floating point instructions cannot use general purpose registers.
Only floating point instructions may be used with the floating point registers.

Question 2

(Memory Test:) Why is $f0 not hard-wired to contain a floating point zero, like register $0 is hard-wired to contain an integer zero?

Answer

Because floating point zero has the same representation as integer zero, 32 zero-bits. Register $0 works as a floating point zero as well as an integer zero.

(Floating point "negative zero" has the sign bit set, and all other bits zero. It is rarely needed.)

Double precision

MIPS also has hardware for double precision (64 bit) floating point operations. For this, it uses pairs of single precision registers to hold operands. There are 16 pairs, named $f0, $f2, ... , $f30. Only the even numbered register is specified in a double precision instruction; the odd numbered register of the pair is included automatically.

Some MIPS processors allow only even-numbered registers ($f0, $f2,...) for single precision instructions. However SPIM allows you to use all 32 registers in single precision instructions. These notes follow that usage.

Question 3

Remember the load delay, where it takes an extra machine cycle after a load instruction before integer data reaches a general purpose register? Do you think there is a load delay for floating point load operations?

Answer

Yes.

Single precision load

Actual hardware has a delay between a load instruction and the time when the data reaches the register. The electronics of main memory handles all bit patterns in the same way, so there is the same delay no matter what the bit patterns represent.

In SPIM there is an option that disables the load delay. For this chapter, disable the load delay. (Floating point is tricky enough already).

Loading a single precision value is done with a pseudoinstruction:

l.s   fd,addr     # load register fd from addr
                  # (pseudoinstruction)

This instruction loads 32 bits of data from address addr into floating point register $fd (where $fd is $f0, $f1, ... $f31. Whatever 32 bits are located at addr are copied into fd. If the data makes no sense as a floating point value, that is OK for this instruction. Later on the mistake will be caught when floating point operations are attempted.

Question 4

Every one of the 2³² patterns that 32 bits can form is a legal two's complement integer.

Are some 32-bit patterns not legal as floating point values? Hint: think about how zero is represented.

Answer

Some 32-bit patterns are not legal floating point.

It is not legal to have an exponent field of zero with a non-zero mantissa. There are other combinations that are also illegal.

Single precision store

Sometimes the floating point registers are used as temporary registers for integer data. For example, rather than storing a temporary value to memory, you can copy it to an unused floating point register. This is OK, as long as you don't try to do floating point math with the data.

There is a single precision store pseudoinstruction:

s.s   fd,addr     # store register fd to addr
                  # (pseudoinstruction)

Whatever 32 bits are in fd are copied to addr.

In both of these pseudoinstructions the address addr can be an ordinary symbolic address, or an indexed address.

Question 5

Why would you want to copy a temporary integer value to a floating point register?

Answer

To free up a general purpose register for some other use.

(You might also push the register's contents on the run-time stack, and later pop it back into the register.)

Floating point load immediate

There is a floating point load immediate pseudoinstruction. This loads a floating point register with a constant value that is specified in the instruction.

li.s   fd,val     # load register $fd with val
                  # (pseudoinstruction)

Here is a code snippet showing this:

li.s    $f1,1.0             # $f1 = constant 1.0
li.s    $f2,2.0             # $f2 = constant 2.0
li.s    $f10,1.0e-5         # $f10 = 0.00001

Question 6

(Take a guess:) Could the first instruction be written as li.s $f1,1?

Answer

No. The decimal point is needed in the constant (at least for SPIM). This, of course, depends on which assembler you are using.

Example program

Here is a program that exchanges (swaps) the floating point values at valA and valB. Notice how the two floating point values are written. The first in the ordinary style; the second in scientific notation.

## swap.asm
##
## Exchange the values in valA and valB

        .text
        .globl  main

main:
        l.s     $f0,valA        # $f0  <-- valA
        l.s     $f1,valB        # $f1  <-- valB
        s.s     $f0,valB        # $f0  --> valB
        s.s     $f1,valA        # $f1  --> valA

        li      $v0,10          # code 10 == exit
        syscall                 # Return to OS.
                
        .data
valA:   .float  8.32            # 32 bit floating point value
valB:   .float  -0.6234e4       # 32 bit floating point value
                                # small 'e' only

Question 7

(Thought Question:) Can a general purpose register hold a floating point value?

Answer

Yes. A general purpose register can hold any 32-bit pattern.

Full-word aligned

However if you want to perform floating point arithmetic, then the floating point number must be in a floating point register.

The previous program exchanged the bit patterns held at two memory locations. It could just as easily been written using general purpose registers since no arithmetic was done with the bit patterns in the registers:

## swap.asm
##
## Exchange the values in valA and valB

        .text
        .globl  main

main:
        lw      $t0,valA        # $t0  <-- valA
        lw      $t1,valB        # $t1  <-- valB
        sw      $t0,valB        # $t0  --> valB
        sw      $t1,valA        # $t1  --> valA

        li      $v0,10          # code 10 == exit
        syscall                 # Return to OS.
                
        .data
valA:   .float  8.32            # 32 bit floating point value
valB:   .float  -0.6234e4       # 32 bit floating point value
                                # small 'e' only

For both single precision load and store instructions (as with the general purpose load and store instructions) the memory address must be full-word aligned. It must be a multiple of four. Ordinarily this is not a problem. The assembler takes care of this.

Question 8

Do you think that the SPIM service that prints an integer can be used for floating point values?

Answer

No. The print integer method works correctly only with 32-bit two's complement representation.

Floating point services

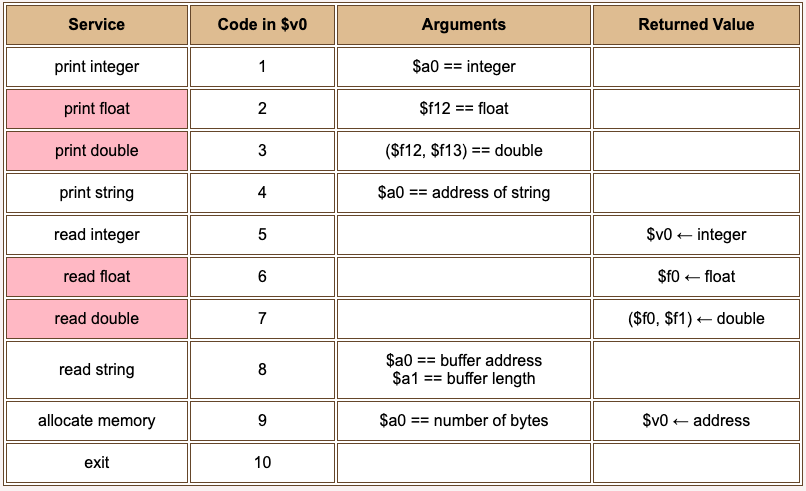
To print a floating point value to the SPIM monitor, use service 2 (for single precision) or service 3 (for double precision). To read a floating point value from the user, use service 6 (for single precision) or service 7 (for double precision). These notes deal mostly with single precision.

Here is the complete list of SPIM exception handler services. Each I/O method uses a specific format for data. The methods for double use an even-odd pair of registers.

Question 9

(Review:) Into what register do you put the service code before executing a syscall.

Answer

Mistake

Depending on the service, you may have to place arguments in other registers as well. The following example program prints out a floating point value. It first does this correctly (using system call 2). Then does it incorrectly uses the integer print service (system call 1). Of course, the 32 bits of the floating point value can be interpreted as an integer, so system call 2 innocently does what we asked it to do.

## print.asm
##
## Print out a 32 bit pattern, first as a float,
## then as an integer.

        .text
        .globl  main

main:
        l.s     $f12,val        # use the float as an argument
        li      $v0,2           # code 2 == print float
        syscall                 # (correct)

        li      $v0,4           # print
        la      $a0,lfeed       # line separator
        syscall

        lw      $a0,val         # use the float as a int
        li      $v0,1           # code 2 == print int
        syscall                 # (mistake)

        li      $v0,10          # code 10 == exit
        syscall                 # Return to OS.
                
        .data
val :   .float  -8.32           # floating point data
lfeed:  .asciiz "\n"

Question 10

Will the assembler catch this error? Will the program bomb when it runs?

Answer

The assembler will not catch this mistake, and the program will run to completion. However, the second print method call writes an incorrect value to the screen.

No type checking

This type of mistake often happens when programming in "C" where type checking is weak. Sometimes the wrong type can be passed to a function (such as printf) and odd things happen.

Compilers that keep track of the data types of values and that make sure that the correct types are used as arguments do strong type checking. Java is strongly typed. In assembly language type checking is largely absent.

Question 11

The first line of output shows the 32 bits interpreted as a single precision floating point value. Is this output correct? (Hint: look at the program on the previous page).

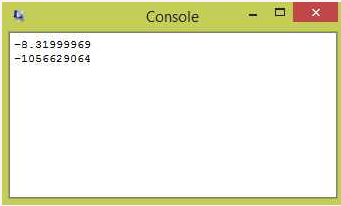
Answer

Maybe Not. The source file for the program specified the constant -8.32 but the program printed -8.31999969

Precision of single precision floats

There are two things wrong: (1) the value -8.32 can not be represented exactly in binary, and (2) the last digit or two of the printed value are likely in error.

Single precision floats have (recall) only 24 bits of precision. This is the equivalent of 7 to 8 decimal digits. SPIM should have printed -8.3199999 to the window.

The 7 or 8 decimal digits of precision is much worse than most electronic calculators. It is usually unwise to use single precision floating point in programs. (But these chapters use it since the goal is to explain concepts, not to write production grade programs). Double precision has 15 or 16 decimal places of precision.

Question 12

How many decimal places of precision does Java's primitive type float have? How many decimal places of precision does C's data type float have?

Answer

The answer is the same for both: 7 or 8 places, same as MIPS. All three use the same IEEE standard for single precision float. (But be careful: some C compilers allow you to specify how many bits of precision you want for various data types. Also, C implemented on a weird machine might be non-standard).

Single precision arithmetic

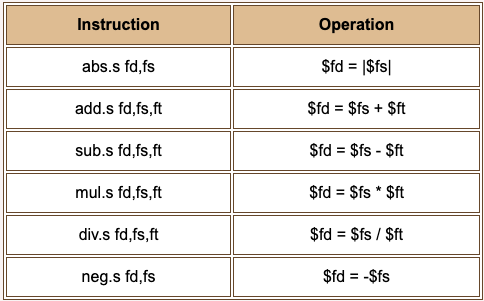
Here are some single precision arithmetic instructions. Each of these corresponds to one machine instruction. There is a double precision version of each instruction that has a "d" in place of the "s". So add.s becomes add.d and corresponds to the machine code that adds two double precision registers.

The first instruction computes the absolute value (makes a positive value) of the value in register $fs.

If the data in an operand register is illegal or an illegal operation is performed (such as division by zero) an exception is raised. The IEEE 754 standard describes what is done in these situations.

Question 13

(Thought Question:) How does the abs.s instruction alter the 32-bit pattern of the float?

Answer

It clears (makes zero) the sign bit, bit 31. All the other bits stay the same.

Data movement

There are three instructions that move data between registers inside the processor:

These instructions merely copy bit patterns between registers. The pattern is not altered. With the mfc1 instruction, the contents of a floating point register is copied "as is" to a general purpose register. So a complicated calculation with integers can use float registers to hold intermediate results. (But the float registers cannot be used with integer instructions.) And a complicated calculation with floats can use general purpose registers the same way. (But the general purpose registers cannot be used with floating point instructions.)

Question 14

(Thought Question:) The neg.s fd,fs instruction places the negation of the number in $fs into $fd. How does it do this?

Answer

The neg.s fd,fs instruction toggles the sign bit of the float in $fs when it copies the pattern to $fd.

Example program

Here is a program that serves no practical purpose except as an example. The program loads a general purpose register with a two's complement 1 and copies that pattern to a floating point register. Then it loads a floating point register with an IEEE 1.0 and moves that pattern to a general purpose register.

## Move data between the coprocessor and the CPU

        .text
        .globl main

main:   
        li      $t0,1           # $t0 <-- 1
                                # (move to the coprocessor)
        mtc1    $t0,$f0         # $f0 <-- $t0 
        
        li.s    $f1,1.0         # $f1 <-- 1.0
                                # (move from the coprocessor)
        mfc1    $t1,$f1         # $t1 <-- $f1 
        
        li      $v0,10          # exit
        syscall

Here is what the SPIM registers contain after running the program:

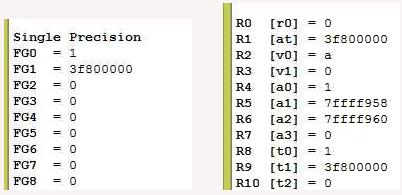
The bit pattern 00000001 is the two's complement representation of one. It is now in registers $t0 and $f0.

The bit pattern 3f800000 is the IEEE representation of 1.0. That pattern is now in registers $f1 and $t1. (It is also in register $at which is used in implementing the pseudoinstruction li.s).

Question 15

Could floating point arithmetic be done with the value in register $f0? Inspect the contents for FP0 in the SPIM register display.

Answer

No. A biased exponent of all zeros requires that the mantissa be all zeros.

Example program: polynomial evaluation

The example program computes the value of ax² + bx + c. It starts by asking the user for x:

        .text
        .globl main

main:   # read input
        la      $a0,prompt          # prompt user for x
        li      $v0,4               # print string
        syscall
        
        li      $v0,6               # read single
        syscall                     # $f0 <-- x
        
        # evaluate the quadratic
        . . . . .
 
        .data
        . . . . .
                
prompt: .asciiz "Enter x: "

After the syscall the floating point value from the user is in $f0. The next section of the program does the calculation.

Question 16

Should a, b, and c be integer constants or floating point constants?

Answer

Floating point constants.

Evaluation

Here is the part of the code that evaluates the polynomial. Remember that x is in $f0.

        # Register Use Chart
        # $f0 -- x
        # $f2 -- sum of terms
        . . . . . 
        
        # evaluate the quadratic
        l.s     $f2,a               # sum = a
        mul.s   $f2,$f2,$f0         # sum = ax
        
        l.s     $f4,bb              # get b
        add.s   $f2,$f2,$f4         # sum = ax + b
        mul.s   $f2,$f2,$f0         # sum = (ax+b)x = ax^2 + bx
        
        l.s     $f4,c               # get c
        add.s   $f2,$f2,$f4         # sum = ax^2 + bx + c
        . . . . . .

        .data
a:      .float  1.0
bb:     .float  1.0
c:      .float  1.0

The assembler objects to the symbolic address "b" (because there is a mnemonic "b", for branch) so use "bb" instead.

The polynomial is evaluated from left to right. First ax + b is calculated. Then that is multiplied by x and c is added in, giving axx + bx + c.

The value x² is not explicitly calculated. This way of calculating a polynomial is called Horner's Method. It is useful to have in your bag of tricks.

Question 17

Why (do you suppose) are the constants a, b, and c set to 1.0?

Answer

To make debugging easy.

Printing out the result

Here is the final section of the code.

        . . . . . 
                
        # print the result
        mov.s   $f12,$f2            # $f12 = argument
        li      $v0,2               # print single
        syscall

        la      $a0,newl            # new line
        li      $v0,4               # print string
        syscall

        li      $v0,10              # code 10 == exit
        syscall                     # Return to OS.

        .data
        . . . . .

blank:  .asciiz " "
newl:   .asciiz "\n"
        . . . . .

There is nothing new in this code.

Question 18

If x = 0.1 what is ax² + bx + c when a = b = c = 1?

Answer

0.01 + 0.1 + 1.0 = 1.11, you would hope.

Complete program

As we have seen before, the results are not quite accurate. You would expect this because 0.1 cannot be represented accurately.

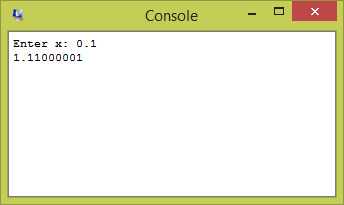
Here is the complete program, suitable for you to copy into a text editor and to play with:

## float1.asm -- compute ax^2 + bx + c for user-input x 
##
## SPIM settings: pseudoinstructions: ON, branch delays: OFF,
##                load delays: OFF

        .text
        .globl main

        # Register Use Chart
        # $f0 -- x
        # $f2 -- sum of terms

main:   # read input
        la      $a0,prompt          # prompt user for x
        li      $v0,4               # print string
        syscall
        
        li      $v0,6               # read single
        syscall                     # $f0 <-- x
        
        # evaluate the quadratic
        l.s     $f2,a               # sum = a
        mul.s   $f2,$f2,$f0         # sum = ax
        l.s     $f4,bb              # get b
        add.s   $f2,$f2,$f4         # sum = ax + b
        mul.s   $f2,$f2,$f0         # sum = (ax+b)x = ax^2 +bx
        l.s     $f4,c               # get c
        add.s   $f2,$f2,$f4         # sum = ax^2 + bx + c
        
        # print the result
        mov.s   $f12,$f2            # $f12 = argument
        li      $v0,2               # print single
        syscall

        la      $a0,newl            # new line
        li      $v0,4               # print string
        syscall

        li      $v0,10              # code 10 == exit
        syscall                     # Return to OS.
        
##
##  Data Segment  
##
        .data
a:      .float  1.0
bb:     .float  1.0
c:      .float  1.0

prompt: .asciiz "Enter x: "
blank:  .asciiz " "
newl:   .asciiz "\n"

Question 19

Had enough?

Answer

Precisely.

Chapter quiz

Question 1

What advantage does 64-bit double precision have over 32-bit single precision?

(A) Increased precision.
(B) A greater range of values is covered.
(C) Greater speed.
(D) Increased precision and a greater range of values.

Answer

Question 2

How many single precision floating point registers does MIPS have?

(A) 8
(B) 16
(C) 32
(D) 64

Answer

Question 3

What is special about register $f0?

(A) It always holds a floating point zero.
(B) It always holds an integer zero.
(C) It gets the results of a multiply operation.
(D) Nothing is special about it.

Answer

Question 4

With actual hardware is there a load delay associated with loading a floating point register from memory?

(A) No. Only integers cause a load delay.
(B) No. Load delays do not apply to coprocessor 0.
(C) Yes. To main memory a floating point representation is just a bit pattern like any other.
(D) Yes. Floating point bits take longer to move.

Answer

Question 5

Does each possible 32-bit pattern represent a single precision float?

(A) No. Most 32-bit patterns represent only integers.
(B) No. Some 32-bit patterns put illegal values in the fields of the float.
(C) Yes. Each possible 32-bit patterns represents a particular float.
(D) Yes. But some numbers are represented by several 32-bit patterns.

Answer

Question 6

Which of the following program fragments copies a floating point value from spotA to spotB?

(A)
```
l.s $f4,spotA
s.s $f4,spotB
```
(B)
```
s.s $f4,spotB
l.s $f4,spotA
```
(C)
```
lf $f4,spotA
sf $f4,spotB
```
(D)
```
li.f $f4,spotA
si.f $f4,spotB
```

Answer

Question 7

Can a general purpose register be used with a floating point instruction?

(A) Yes, as long as the bit pattern in it represents a float.
(B) Yes, as long as at least one other operand is in a floating point register.
(C) No. It can hold a floating point representation, but can't be used in a floating point operation.
(D) No. General purpose registers can't hold floating point representations.

Answer

Question 8

A single precision float has 24 bits of precision. This is equivalent to how many digits in a decimal representation?

(A) 7 or 8
(B) 9 or 10
(C) 12
(D) 24 or 25

Answer

Question 9

Which of the following code fragments subtracts valB from valA, ensures that the result is positive, and stores the result in result?

(A)

l.s   $f6,valA
l.s   $f8,valB
sub.s $f4,$f6,$f8
abs.s $f4
s.s   $f4,result

(B)

l.s   $f6,valA
l.s   $f8,valB
sub.s $f4,$f6,$f8
abs.s $f4,$f4
s.s   $f4,result

(C)

li.s   $f6,valA
li.s   $f8,valB
sub.s $f4,$f6,$f8
abs.s $f4,$f4
sf.s   $f4,result

(D)

l.s   $f6,valB
l.s   $f8,valA
sub.s $f4,$f6,$f8
abs.s $f4,$f4
s.s   $f4,result

Answer

Question 10

Here is a polynomial ax³ + bx² + cx + d. Factor this polynomial to show how it would be evaluated using Horner's method.

(A) x( x( ax + b) + c) + d
(B) cx + d + ax³ + bx²
(C) x3( a + bx^-1) + cx^-2) + d
(D) (a + b + c + d)(x³ + x² + x¹ + 1)

Answer

Programming exercises

NOTE: If you have read the chapters on subroutine linkage, write each exercise as a main program calling a subroutine. Use either the stack-based linkage or the frame-based linkage convention.

In the Settings menu of SPIM set Bare Machine OFF, Allow Pseudo Instructions ON, Load Trap File ON, Delayed Branches OFF, Delayed Loads OFF, Mapped IO ON, Quiet OFF.

Exercise 1 - arithmetic expression

Write a program that computes value of the following arithmetic expression for values of x and y entered by the user:

5.4xy - 12.3y + 18.23x - 8.23

Exercise 2 - harmonic series

Write a program that computes the sum of the first part of the harmonic series:

1/1 + 1/2 + 1/3 + 1/4 + ...

This sum gets bigger and bigger without limit as more terms are added in. Ask the user for a number of terms to sum, compute the sum and print it out.

Exercise 3 - web page RGB colors

Colors on a Web page are often coded as a 24 bit integer as follows:

RRGGBB

In this, each R, G, or B is a hex digit 0..F. The R digits give the amount of red, the G digits give the amount of green, and the B digits give the amount of blue. Each amount is in the range 0..255 (the range of one byte). Here are some examples:

Another way that color is sometimes expressed is as three fractions 0.0 to 1.0 for each of red, green, and blue. For example, pure red is (1.0, 0.0, 0.0), medium gray is (0.5, 0.5, 0.5) and so on.

Write a program that has a color number declared in the data section and that writes out the amount of each color expressed as a decimal fraction. Put each color number in 32 bits, with the high order byte set to zeros:

          .data
color:    .word  0x00FF0000     # pure red, (1.0, 0.0, 0.0)

For extra fun, write a program that prompts the user for a color number and then writes out the fraction of each component.

Exercise 4 - polynomial evaluation (Horner's Method)

Write a program that computes the value of a polynomial using Horner's method. The coefficients of the polynomial are stored in an array of single precision floating point values:

          .data
n:        5
a:        .float 4.3, -12.4, 6.8, -0.45, 3.6

The size and the values in the array may change. Write the program to initialize a sum to zero and then loop n times. Each execution of the loop, with loop counter j, does the following:

sum = sum*x + a[j]

To test and debug this program, start with easy values for the coefficients.

Floating Point Comparison Instructions

The MIPS Floating Point Accelerator (FPA) chip (now, usually part of the processor chip) has a condition bit that is set to 0 or 1 to indicate if a condition is false or true. Several FPA instructions affect this bit and several CPU instructions test this bit.

Chapter Topics:

Comparison instructions: c.eq.s, c.lt.s, c.le.s
Branch instructions: bc1f, bc1t
The Condition bit
Newton's method

Question 1

Are the FPA (floating point accelerator) and coprocessor 1 the same?

Answer

Yes.

FPA chip

In the early days of MIPS, floating point was done on a separate chip. Special instructions were used to bridge the gap between the two chips (such as the two move instructions mtc1 and mfc1 we have already seen). Although these days there is usually just one processor chip, some of the instructions act as if the chips were separate.

Question 2

(Thought Question:) Do you think that testing if two floating point values are equal is a common thing to do?

Answer

Maybe.

Comparison instructions

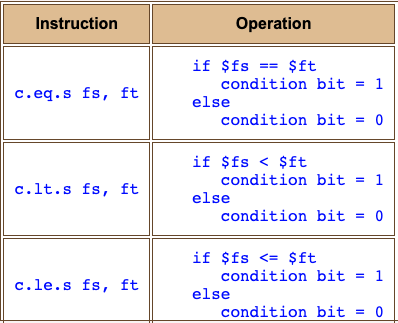
Testing if two floating point numbers are exactly equal is sometimes NOT a good idea. Floating point calculations are not exact. Sometimes values are not equal even though mathematically they should be. It is best to use "less than" or "less than or equal" instead of testing for exact equality. The table shows some MIPS comparison instructions for single precision floating point.

These instructions change the value in the condition bit, a part of the processor. The condition bit is set (made equal to one) if the condition is true. Otherwise the condition bit is cleared (made equal to zero). There are more comparison operations than these. But these notes use just these three. The others involve the various IEEE 754 codes for exceptional results.

Question 3

There is no "greater than" instruction! What can we do?

Answer

Use "less than" with the operations reversed.

Branch instructions

The floating point branch instructions inspect the condition bit in the coprocessor. The bc1t instruction takes the branch if the bit is true (==1). The bc1f instruction takes the branch if the bit is false (==0). These are the only two floating point branch instructions.

The branch instructions have a one instruction branch delay. Hardware requires a nop instruction after each branch instruction. For this chapter, let us not bother with this. When running the programs with SPIM, disable branch delays in the settings menu.

Question 4

Where does execution of the bc1t instruction take place? In the FPU or the CPU?

Answer

The CPU. Although the instruction tests a bit in the FPU, it affects the program counter of the CPU and takes place in the CPU.

Example

The example program looks at two floating point values, A and B, and writes a message saying which one is smallest. First the program loads the two values A and B into registers:

main:   # get the values into registers
        l.s     $f0,A
        l.s     $f2,B
        . . . . 
    
A:      .float  4.830
B:      .float  1.012
        . . . . 

Then the program tests if A<B, or if B<A. If neither of these is true, then it must be that B==A.

        . . . .
        c.lt.s  $f0,$f2          # is A < B?
        bc1t    printA           # yes:  print A

        c.lt.s  $f2,$f0          # is B < A?
        bc1t    printB           # yes:  print B

        la      $a0,EQmsg        # otherwise
        li      $v0,4            # they are equal
        . . . . 

(Remember that for this chapter, branch delays have been turned off in SPIM.)

Question 5

The three outcomes can be detected by other comparison instructions. Here is another arrangement of the code:

Fill in the blanks. You may wish to consult the list of floating point comparison instructions.

Answer

        c.eq.s  $f0,$f2          # is A = B?
        bc1t    printEQ          # yes: print equal

        c.lt.s  $f2,$f0          # is B < A?
        bc1t    printB           # yes: print B

                                 # otherwise A < B

The complete program

Here is the complete program. There is nothing new in the remainder of the code.

## min.asm --- determine the min of two floats
##
        .text
        .globl main

main:   # get the values into registers
        l.s     $f0,A
        l.s     $f2,B
        
        c.lt.s  $f0,$f2          # is A < B?
        bc1t    printA           # yes -- print A
        c.lt.s  $f2,$f0          # is B < A?
        bc1t    printB           # yes -- print B

        la      $a0,EQmsg        # otherwise
        li      $v0,4            # they are equal
        syscall
        mov.s   $f12,$f0         # print one of them
        b       prtnum
        
printA: la      $a0,Amsg         # message for A
        li      $v0,4
        syscall
        mov.s   $f12,$f0         # print A
        b       prtnum
        
printB: la      $a0,Bmsg         # message for B
        li      $v0,4
        syscall
        mov.s   $f12,$f2         # print B
        
prtnum: li      $v0,2            # print single precision
                                 # value in $f12
        syscall
        la      $a0,newl
        li      $v0,4            # print new line
        syscall
        jr      $ra              # return to OS

        .data

A:      .float  4.830
B:      .float  1.012
Amsg:   .asciiz "A is smallest: "
Bmsg:   .asciiz "B is smallest: "
EQmsg:  .asciiz "They are equal: "
newl:   .asciiz "\n"

Question 6

Would you expect the condition bit (of the FPU) to keep its value until it is altered by another comparison instruction?

Answer

Yes.

Condition bit holds its value

The condition bit is like a one bit register. It continues to hold the value put into it by a comparison instruction until another comparison instruction is executed. The following code ensures that register $f12 has the minimum of $f0 or $f2. If they are equal, then $f12 gets the value they both contain.

main:   l.s     $f0,A            # get the values 
        l.s     $f2,B            # into registers
        
        c.lt.s  $f0,$f2          # is A < B?
        mov.s   $f12,$f0         # move A to $f12
                                 # (condition bit continues to hold
                                 # its value)
        bc1t    common           # otherwise
        mov.s   $f12,$f2         # move B to $f12

common:

The above code is contrived; it would be better to reverse the third and fourth statements. However, sometimes it is very useful to hold the condition bit's value for several instructions before using it.

Question 7

(Review:) should c.eq.s be used to implement a while loop?

Answer

No, not usually. With the inherent inaccuracy of floating point this risks creating a non-terminating loop. This next example shows a while loop.

Newton's method

Newton's method is a way to compute the square root of a number. Say that n is the number and that x is an approximation to the square root of n. Then:

x' =(1/2)(x + n/x)

x' is an even better approximation to the square root. The reasons for this are buried in your calculus book (which you, perhaps, have buried in the darkest corner of your basement). But, to make the formula plausible, look what happens if the approximation x happens to be exactly the square root. In other words, what if x = n^0.5. Then:

x' = (1/2)(x + n/x) = (1/2)( n^0.5 + n/n^0.5 )
   = (1/2)(n^0.5 + n^0.5) = n^0.5

If x reaches the exact value, it stays fixed at that value.

Question 8

Try it: Say that n == 4 and that our first approximation to the square root is x == 1. Use the formula to get the next approximation:

x' =(1/2)(1 + 4/1)

Answer

x = 2.5, a better approximation to the square root of 4.0.

Start of the program

Now using x = 2.5 in the formula yields:

x' = (1/2)(2.5 + 4/2.5) = (1/2)(2.5 + 1.6) = (1/2)(4.1) = 2.05

This is a better yet approximation, and could be fed back into the formula to get an even better approximation.

The example program implements this procedure. It repeatedly uses the formula to calculate increasingly accurate approximations to the square root. Here is the start of the program:

## newton.asm -- compute sqrt(n) 

## given an approximation x to sqrt(n),
## an improved approximation is:

## x' = (1/2)(x + n/x)

## $f0  ---  n
## $f1  ---  1.0
## $f2  ---  2.0
## $f3  ---  x  : current approx.
## $f4  ---  x' : next approx.
## $f8  ---  temp
## $f10 ---  accuracy limit, a small value

        .text
        .globl main

main:   

        l.s     $f0,n               # get n
        li.s    $f1,1.0             # constant 1.0
        li.s    $f2,2.0             # constant 2.0
        li.s    $f3,1.0             # x == first approx.
        li.s    $f10,1.0e-5         # accuracy limit
loop:

The program will be written so that it stops looping when no further improvement is possible. We can't expect to get the answer exactly correct.

Question 9

(Memory test:) How many decimal places of precision can be expected with floating point?

Answer

Six or seven. To be safe, count on no better than six digits of accuracy. This program uses five place accuracy.

Apply the formula

The value in f10 is used to test if the five digits of accuracy have been reached. We will do this in a moment. Here is the part of the program that uses the formula:

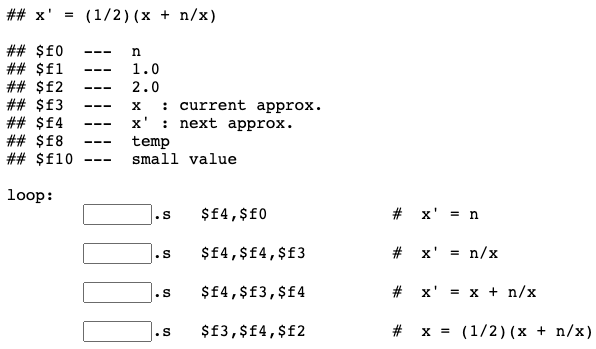
Question 10

But part of each mnemonic is missing! Fill them in. You may wish to look at floating point operations.

Answer

See below.

Ending the loop

## x' = (1/2)(x + n/x)

## $f0  ---  n
## $f1  ---  1.0
## $f2  ---  2.0
## $f3  ---  x  : current approx.
## $f4  ---  x' : next approx.
## $f8  ---  temp
## $f10 ---  small value

loop:   
        mov.s   $f4,$f0             #  x' = n
        div.s   $f4,$f4,$f3         #  x' = n/x
        add.s   $f4,$f3,$f4         #  x' = x + n/x
        div.s   $f3,$f4,$f2         #  x = (1/2)(x + n/x)

        # test if loop should end

After calculating a new approximation it is time to see if the loop should end. This is more work than the actual calculation. We can't test if we have the exact answer yet, because that may never happen. Instead let us test if the current x is close to the square root of n.

Question 11

Say that x is very close to n^0.5. What do you think will be the value of n/(x*x)?

Answer

It should be very close to 1.0.

Ending test

But due to the lack of precision with floating point, the best we can hope for is to calculate an x such that:

0.999999  <  n/(x*x)  <  1.00001

The left and the right bound in the above have 6 decimal digits of precision. If 1.00000 is subtracted from this value the result is:

-0.000001  <  n/(x*x) - 1  <  0.00001

To be safe, terminate the loop when:

| n/(x*x) - 1 |  <  0.00001

... where |x| means the absolute value of x.

Question 12

Is there a floating point absolute value instruction?

Answer

Yes.

Code for ending test

Here is the code for ending the loop when | n/(x*x) - 1 | < 0.00001.

## $f0  ---  n
## $f1  ---  1.0
## $f2  ---  2.0
## $f3  ---  x  : current approx.
## $f4  ---  x' : next approx.
## $f8  ---  temp
## $f10 ---  small value

        mul.s   $f8,$f3,$f3         # x*x
        div.s   $f8,$f0,$f8         # n/(x*x)
        sub.s   $f8,$f8,$f1         # n/(x*x) - 1.0
        abs.s   $f8,$f8             # |n/(x*x) - 1.0|
        c.lt.s  $f8,$f10            # |n/(x*x) - 1.0| < small ?
        bc1t    done                # yes: done
  
        j       loop
        
done:

Question 13

Is this program commercial quality code?

Answer

Not even close. Numerical analysis is tricky. You should use a square root method from a package of mathematical subroutines if you really need one.

Complete program

But it is good enough for a demonstration on the SPIM simulator. Here is the complete program. Copy it to your editor, save it to a file, and play with it in SPIM.

## newton.asm -- compute sqrt(n) 

## given an approximation x to sqrt(n),
## an improved approximation is:

## x' = (1/2)(x + n/x)

## $f0  ---  n
## $f1  ---  1.0
## $f2  ---  2.0
## $f3  ---  x  : current approx.
## $f4  ---  x' : next approx.
## $f8  ---  temp

        .text
        .globl main

main:   

        l.s     $f0,n               # get n
        li.s    $f1,1.0             # constant 1.0
        li.s    $f2,2.0             # constant 2.0
        li.s    $f3,1.0             # x == first approx.
        li.s    $f10,1.0e-5         # five figure accuracy

loop:   
        mov.s   $f4,$f0             # x' = n
        div.s   $f4,$f4,$f3         # x' = n/x
        add.s   $f4,$f3,$f4         # x' = x + n/x
        div.s   $f3,$f4,$f2         # x    = (1/2)(x + n/x)

        mul.s   $f8,$f3,$f3         # x^2
        div.s   $f8,$f0,$f8         # n/x^2
        sub.s   $f8,$f8,$f1         # n/x^2 - 1.0
        abs.s   $f8,$f8             # |n/x^2 - 1.0|
        c.lt.s  $f8,$f10            # |x^2 - n| < small ?
        bc1t    done                # yes: done
  
        j       loop                # next approximation
        
done:
        mov.s   $f12,$f3            # print the result
        li      $v0,2
        syscall
                
        jr      $ra                 # return to OS

##
##  Data Segment  
##
        .data
n:      .float  3.0

Question 14

What result do you expect if this program calculated the square root of 4.000000e+6?

Answer

You should expect 2.0000e+3 or so, to five places of precision.

Chapter quiz

Question 1

How does a floating point comparison instruction indicate that a certain condition is true?

(A) It sets the condition bit to zero.
(B) It sets the condition bit to one.
(C) It sets a designated register to one.
(D) It executes a branch.

Answer

Question 2

Why is it often unwise to test if two floating point values are equal?

(A) Floating point values are often approximations so equality sometimes does not occur where mathematically it should.
(B) Because there is more information in testing if one value is larger than another.
(C) Because equality is not defined for floating point values.
(D) Because testing for equality is time consuming.

Answer

Question 3

After the condition bit is set (or cleared), how long does it retain its value?

(A) Forever.
(B) For one instruction cycle.
(C) Until it is tested in a branch instruction.
(D) Until another comparison instruction changes it.

Answer

Question 4

Which set of instructions branches to label if the contents of $f0 are less than the contents of `$ f2`?

(A)
```
c.lt.s  $f0, $f2
bc1f    label
```
(B)
```
c.lt.s  $f2, $f0
bc1t    label
```
(C)
```
c.lt.s  $f0, $f2
bc1t    label
```
(D)
```
c.le.s  $f0, $f2
bc1t    label
```

Answer

Question 5

Which set of instructions branches to label if the contents of $f0 are greater or equal to the contents of $f2?

(A)
```
c.ge.s  $f0, $f2
bc1t    label
```
(B)
```
c.lt.s  $f2, $f0
bc1t    label
```

(C)

c.eq.s  $f0, $f2
bc1t    label
c.gt.s  $f0, $f2
bc1t    label

(D)
```
c.le.s  $f2, $f0
bc1t    label
```

Answer

Question 6

Which of the following code segments branches to label if 0.0 < x?

(A)

        l.s     $f6,x
        li.s    $f0,0.0
        c.lt.s  $f6,$f0
        bc1t    label

(B)

        l.s     $f6,x
        li.s    $f6,0.0
        c.lt.s  $f0,$f6
        bc1t    label

(C)

        l.s     $f6,x
        li.s    $f0,0.0
        c.lt.s  $f0,$f6
        bc1t    label

(D)

        li.s    $f6,x
        li.s    $f0,0.0
        c.lt.s  $f0,$f6
        bc1t    label

Answer

Question 7

Which of the following code segments branches to label if 0.0 < x < 10.0?

(A)

        l.s     $f6,x
        li.s    $f0,0.0
        c.lt.s  $f6,$f0
        bc1f    fail
        li.s    $f0,10.0
        c.lt.s  $f6,$f0
        bc1t    label
fail:   . . .

label:  . . .

(B)

        l.s     $f6,x
        li.s    $f0,0.0
        c.lt.s  $f0,$f6
        bc1f    fail
        li.s    $f0,10.0
        c.lt.s  $f6,$f0
        bc1t    label
fail:   . . .

label:  . . .

(C)

        l.s     $f6,x
        li.s    $f0,0.0
        c.lt.s  $f0,$f6
        bc1f    fail
        li.s    $f0,10.0
        c.lt.s  $f0,$f6
        bc1t    label
fail:   . . .

label:  . . .

(D)

        l.s     $f6,x
        li.s    $f0,0.0
        c.le.s  $f0,$f6
        bc1f    fail
        li.s    $f0,10.0
        c.le.s  $f6,$f0
        bc1t    label
fail:   . . .

label:  . . .

Answer

Question 8

What is the method that is often used for computing square root?

(A) Newton's Method
(B) Cauchy's Method
(C) Pascal's Method
(D) Elimination Method

Answer

Question 9

About how many decimal places of accuracy does single precision floating point have?

(A) 3 or 4
(B) 4 or 5
(C) 6 or 7
(D) 8 or 9

Answer

Question 10

When a floating point value is being computed in a loop, how is the loop usually ended?

(A) After a few iterations.
(B) After very many iterations.
(C) When the computed value exactly matches a specified condition.
(D) When the computed value falls into a specified range.

Answer

Programming exercises

NOTE: If you have read the chapters on subroutine linkage, write each exercise as a main program calling a subroutine. Use either the stack-based linkage or the frame-based linkage convention.

In the Settings menu of SPIM set Bare Machine OFF, Allow Pseudo Instructions ON, Load Trap File ON, Delayed Branches OFF, Delayed Loads OFF, Mapped IO ON, Quiet OFF.

Run the programs by clicking SimulatorGo and then OK in the pop-up panel.

Exercise 1 - exp(x)

Write a program that computes exp(x) by using a Taylor series:

exp(x) = 1 + x + x²/2 + x³/3! + x⁴/4! + ...

The user enters x. exp(x) is e^x, where e is the base of the natural logarithms, 2.718281828... You don't need to worry about the math behind this. Just compute a sum of terms. Each term in the sum looks like:

xⁿ/n!

Designate a register to hold the current term. Initialize it to 1.0 (the zeroeth term). Term one is calculated by multiplying:

term*x/1

Term one is the value x. Term two is calculated by multiplying:

term*x/2

Term two is the value x²/2. Term three is calculated by multiplying:

term*x/3

Term three is the value x³/3!. Term four is calculated by multiplying:

term*x/4

... and so on. In general, after you have added term (n-1) to the sum, calculate term n by multiplying:

term *x/n

Keep doing this in a loop until the term becomes very small. Here are some example runs (with SPIM using single precision). As usual, only the first seven digits printed have any significance.

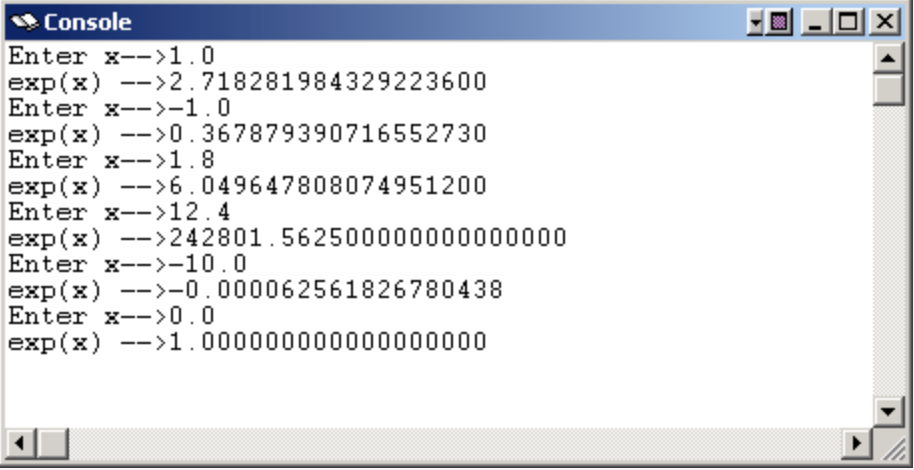
It might be helpful to first write this program in Java or C to verify your design, and then to proceed with the version in assembly language.

Exercise 2 - pi

Various infinite series for pi have been discovered. The first such series was

pi = 4( 1 - 1/3 + 1/5 - 1/7 + 1/9 - . . .)

This series is of little practical value because enormous numbers of terms are required to achieve good approximations (Acton, Calculus, 1999). However, it does provide good programming practice.

Write a SPIM program that writes out the sum of the first 1000, 2000, 3000, ... , 10000 terms of the series.

As with the previous program, write a version of this program in C or Java first to check that your design is correct.

Binary Fractions​

Bit patterns​

Positional notation​

Base two positional notation​

Base two to base ten​

Include or exclude​

Fixed point notation​

Adding fixed point expressions​

Binary addition algorithm works​

Limited precision​

Infinitely many missing numbers​

Shifting left one bit​

Converting representatives from decimal to binary​

Practice​

Non-terminating result​

Dangerous code​

Hidden infinite loop​

Count with integers​

Calculate each float​

Chapter quiz A​

Chapter quiz B​

IEEE 754 Floating Point​

Why floating point?​

Floating point​

Early floating point​

Floating point compatibility​

Scientific notation​

Negative exponents​

Negative values​

e​

Fixed number of digits​

IEEE 754 Floating Point​

More on Ms. Mantissa​

How the mantissa works​

Practice​

The exponent​

Exponent practice​

Float formula​

1.0​

SPIM data​

-0.1​

Chapter quiz​

Floating Point Arithmetic on MIPS​

MIPS floating point​

Double precision​

Single precision load​

Single precision store​

Floating point load immediate​

Example program​

Full-word aligned​

Floating point services​

Mistake​

No type checking​

Precision of single precision floats​

Single precision arithmetic​

Data movement​

Example program​

Example program: polynomial evaluation​

Evaluation​

Printing out the result​

Complete program​

Chapter quiz​

Programming exercises​

Exercise 1 - arithmetic expression​

Exercise 2 - harmonic series​

Exercise 3 - web page RGB colors​

Exercise 4 - polynomial evaluation (Horner's Method)​

Floating Point Comparison Instructions​

FPA chip​

Comparison instructions​

Branch instructions​

Example​

The complete program​

Condition bit holds its value​

Newton's method​

Start of the program​

Apply the formula​

Ending the loop​

Ending test​

Code for ending test​

Binary Fractions

Bit patterns

Positional notation

Base two positional notation

Base two to base ten

Include or exclude

Fixed point notation

Adding fixed point expressions

Binary addition algorithm works

Limited precision

Infinitely many missing numbers

Shifting left one bit

Converting representatives from decimal to binary

Practice

Non-terminating result

Dangerous code

Hidden infinite loop

Count with integers

Calculate each float

Chapter quiz A

Chapter quiz B

IEEE 754 Floating Point

Why floating point?

Floating point

Early floating point

Floating point compatibility

Scientific notation

Negative exponents

Negative values

e

Fixed number of digits

IEEE 754 Floating Point

More on Ms. Mantissa

How the mantissa works

Practice

The exponent

Exponent practice

Float formula

1.0

SPIM data

-0.1

Chapter quiz

Floating Point Arithmetic on MIPS

MIPS floating point

Double precision

Single precision load

Single precision store

Floating point load immediate

Example program

Full-word aligned

Floating point services

Mistake

No type checking

Precision of single precision floats

Single precision arithmetic

Data movement

Example program

Example program: polynomial evaluation

Evaluation

Printing out the result

Complete program

Chapter quiz

Programming exercises

Exercise 1 - arithmetic expression

Exercise 2 - harmonic series

Exercise 3 - web page RGB colors

Exercise 4 - polynomial evaluation (Horner's Method)

Floating Point Comparison Instructions

FPA chip

Comparison instructions

Branch instructions

Example

The complete program

Condition bit holds its value

Newton's method

Start of the program

Apply the formula

Ending the loop

Ending test

Code for ending test