Queues and Stacks
Readings
Queue
Description: Like the line outside a busy restaurant. "First come, first served." A queue stores items in a first-in, first-out (FIFO) order. Picture a queue like the line outside a busy restaurant. First come, first served.
Visual description:
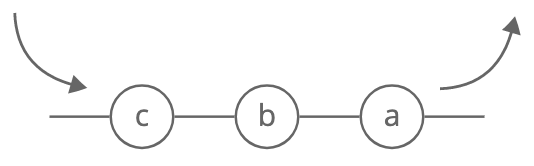
Strengths:
- Fast operations: All queue operations take time.
Uses:
- Breadth-first search uses a queue to keep track of the nodes to visit next.
- Printers use queues to manage jobs—-jobs get printed in the order they're submitted.
- Web servers use queues to manage requests—-page requests get fulfilled in the order they're received.
- Processes wait in the CPU scheduler's queue for their turn to run.
Worst Case Analysis:
| Context | Big O |
|---|---|
| space | |
| enqueue | |
| dequeue | |
| peek |
Implementation
Queues are easy to implement with linked lists:
- To enqueue, insert at the tail of the linked list.
- To dequeue, remove at the head of the linked list.
You could implement a queue with an array or dynamic array, but it would get kinda messy. Try drawing it out. You'll notice that you'd need to build out a "scoot over" or "re-center" operation that automatically fires when your queue items hit the bottom edge of the array.
Stack
Description: Like a stack of dirty plates in the sink. The first one you take off the top is the last one you put down. A stack stores items in a last-in, first-out (LIFO) order. Picture a pile of dirty plates in your sink. As you add more plates, you bury the old ones further down. When you take a plate off the top to wash it, you're taking the last plate you put in. "Last in, first out."
Visual description:
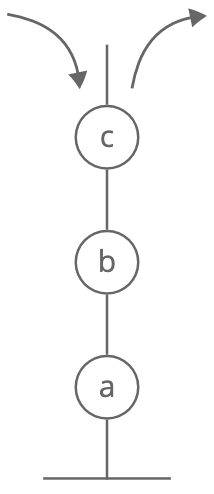
Strengths:
- Fast operations: All stack operations take time.
Uses:
- The call stack is a stack that tracks function calls in a program. When a function returns, which function do we "pop" back to? The last one that "pushed" a function call.
- Depth-first search uses a stack (sometimes the call stack) to keep track of which nodes to visit next.
- String parsing: Stacks turn out to be useful for several types of string parsing.
Worst Case Analysis:
| Context | Big O |
|---|---|
| space | |
| push | |
| pop | |
| peek |
Implementation
You can implement a stack with either a linked list or a dynamic array—-they both work pretty well:
| Stack Push | Stack Pop | |
|---|---|---|
| Linked Lists | insert at head | remove at head |
| Dynamic Arrays | append | remove last element |
Practice
Largest Stack
You want to be able to access the largest element in a stack.
You've already implemented this Stack class:
class Stack(object):
def __init__(self):
"""Initialize an empty stack"""
self.items = []
def push(self, item):
"""Push a new item onto the stack"""
self.items.append(item)
def pop(self):
"""Remove and return the last item"""
# If the stack is empty, return None
# (it would also be reasonable to throw an exception)
if not self.items:
return None
return self.items.pop()
def peek(self):
"""Return the last item without removing it"""
if not self.items:
return None
return self.items[-1]
Use your Stack class to implement a new class MaxStack with a method get_max() that returns the largest element in the stack. get_max() should not remove the item.
Your stacks will contain only integers.
Hint 1
Comments about just-in-time and ahead-of-time approaches
Just-in-time and ahead-of-time are two different approaches for deciding when to do work.
Say we're writing a function that takes in a number between 2 and 1,000 and checks whether the number is prime.
One option is to do the primality check when the function is called:
from math import sqrt
def is_prime_brute_force(n):
highest_possible_factor = int(sqrt(n))
for potential_factor in range(2, highest_possible_factor + 1):
if n % potential_factor == 0:
return False
return True
def is_prime(n):
return is_prime_brute_force(n)
This is a just-in-time approach, since we only test a number when we've received it as input. (We determine whether nn is prime "just in time" to be returned to the caller.)
Another option is to generate all the primes below 1,000 once and store them in a set. Later on, when the function is called, we'll just check if is in that set.
from math import sqrt
def is_prime_brute_force(n):
highest_possible_factor = int(sqrt(n))
for potentialFactor in range(2, highest_possible_factor + 1):
if n % potentialFactor == 0:
return False
return True
primes = set()
for potential_prime in range(2, 1001):
if is_prime_brute_force(potential_prime):
primes.add(potential_prime)
def is_prime(n):
return n in primes
Here we're taking an ahead-of-time approach, since we do the calculations up front before we're asked to test any specific numbers.
So, what's better: just-in-time or ahead-of-time? Ultimately, it depends on usage patterns.
If you expect is_prime() will be called thousands of times, then a just-in-time approach will do a lot of repeat computation. But if is_prime() is only going to be called twice, then testing all those values ahead-of-time is probably less efficient than just checking the numbers as they're requested.
Decisions between just-in-time and ahead-of-time strategies don't just come up in code. They're common when designing systems, too.
Picture this: you've finished a question on Interview Cake and triumphantly click to advance to the next question: Binary Search Tree Checker. Your browser issues a request for the question in JavaScript.
There are a few possibilities for what happens on our server:
- One option would be to store a basic template for Binary Search Tree Checker as a starting point for any language. We'd fill in this template to generate the JavaScript version when you request the page. This is a just-in-time approach, since we're waiting for you to request Binary Search Tree Checker in JavaScript before we do the work of generating the page.
- Another option would be to make separate Binary Search Tree Checker pages for every language. When you request the page in JavaScript, we grab the JavaScript template we made earlier and send it back. This is an ahead-of-time approach, since we generate complete pages before you send a request.
On Interview Cake, we take an ahead-of-time approach to generating pages in different languages. This helps make each page load quickly, since we're processing our content once instead of every time someone visits a page.
A just-in-time approach is to have get_max() simply walk through the stack (popping all the elements off and then pushing them back on) to find the max element. This takes time for each call to get_max(). But we can do better.
Hint 2
To get time for get_max(), we could store the max integer as a member variable (call it max). But how would we keep it up to date?
Hint 3
For every push(), we can check to see if the item being pushed is larger than the current max, assigning it as our new max if so. But what happens when we pop() the current max? We could re-compute the current max by walking through our stack in time. So our worst-case runtime for pop() would be . We can do better.
Hint 4
What if when we find a new current max (new_max), instead of overwriting the old one (old_max) we held onto it, so that once new_max was popped off our stack we would know that our max was back to old_max?
Hint 5
What data structure should we store our set of maxes in? We want something where the last item we put in is the first item we get out ("last in, first out").
Hint 6
We can store our maxes in another stack!
Hint 7 (solution)
Solution
We define two new stacks within our MaxStack class—-stack holds all of our integers, and maxes_stack holds our "maxima." We use maxes_stack to keep our max up to date in constant time as we push() and pop():
- Whenever we
push()a new item, we check to see if it's greater than or equal to the current max, which is at the top ofmaxes_stack. If it is, we alsopush()it ontomaxes_stack. - Whenever we
pop(), we alsopop()from the top ofmaxes_stackif the item equals the top item inmaxes_stack.
class MaxStack(object):
def __init__(self):
self.stack = Stack()
self.maxes_stack = Stack()
def push(self, item):
"""Add a new item onto the top of our stack."""
self.stack.push(item)
# If the item is greater than or equal to the last item in maxes_stack,
# it's the new max! So we'll add it to maxes_stack.
if self.maxes_stack.peek() is None or item >= self.maxes_stack.peek():
self.maxes_stack.push(item)
def pop(self):
"""Remove and return the top item from our stack."""
item = self.stack.pop()
# If it equals the top item in maxes_stack, they must have been pushed
# in together. So we'll pop it out of maxes_stack too.
if item == self.maxes_stack.peek():
self.maxes_stack.pop()
return item
def get_max(self):
"""The last item in maxes_stack is the max item in our stack."""
return self.maxes_stack.peek()
Complexity
time for push(), pop(), and get_max(). additional space, where is the number of operations performed on the stack.
Bonus
Our solution requires additional space for the second stack. But do we really need it?
Can you come up with a solution that requires additional space? (It's tricky!)
What We Learned
Notice how in the solution we're spending time on push() and pop() so we can save time on get_max(). That's because we chose to optimize for the time cost of calls to get_max().
But we could've chosen to optimize for something else. For example, if we expected we'd be running push() and pop() frequently and running get_max() rarely, we could have optimized for faster push() and pop() methods.
Sometimes the first step in algorithm design is deciding what we're optimizing for. Start by considering the expected characteristics of the input.
Implement A Queue With Two Stacks
Implement a queue with 2 stacks. Your queue should have an enqueue and a dequeue method and it should be "first in first out" (FIFO).
Optimize for the time cost of calls on your queue. These can be any mix of enqueue and dequeue calls.
Assume you already have a stack implementation and it gives time push and pop.
Hint 1
Let's call our stacks stack1 and stack2.
To start, we could just push items onto stack1 as they are enqueued. So if our first 3 calls are enqueues of a, b, and c (in that order) we push them onto stack1 as they come in.
But recall that stacks are last in, first out. If our next call was a dequeue() we would need to return a, but it would be on the bottom of the stack.
Hint 2

Look at what happens when we pop c, b, and a one-by-one from stack1 to stack2.

Notice how their order is reversed.
We can pop each item 1-by-1 from stack1 to stack2 until we get to a.
We could return a immediately, but what if our next operation was to enqueue a new item d? Where would we put d? d should get dequeued after c, so it makes sense to put them next to each-other ... but c is at the bottom of stack2.
Hint 3

Let's try moving the other items back onto stack1 before returning. This will restore the ordering from before the dequeue, with a now gone. So if we enqueue d next, it ends up on top of c, which seems right.

So we're basically storing everything in stack1, using stack2 only for temporarily "flipping" all of our items during a dequeue to get the bottom (oldest) element.
This is a complete solution. But we can do better.
What's our time complexity for operations? At any given point we have items inside our data structure, and if we dequeue we have to move all of them from stack1 to stack2 and back again. One dequeue operation thus costs . The number of dequeues is , so our worst-case runtime for these mm operations is .
Not convinced we can have dequeues and also have each one deal with items in the data structure? What if our first operations are enqueues, and the second are alternating enqueues and dequeues. For each of our dequeues, we have items in the data structure.
We can do better than this runtime.
Hint 4
What if we didn't move things back to stack1 after putting them on stack2?
Hint 5 (solution)
Let's call our stacks in_stack and out_stack.
For enqueue, we simply push the enqueued item onto in_stack.
For dequeue on an empty out_stack, the oldest item is at the bottom of in_stack. So we dig to the bottom of in_stack by pushing each item one-by-one onto out_stack until we reach the bottom item, which we return.
After moving everything from in_stack to out_stack, the item that was enqueued the 2nd longest ago (after the item we just returned) is at the top of out_stack, the item enqueued 3rd longest ago is just below it, etc. So to dequeue on a non-empty out_stack, we simply return the top item from out_stack.

With that description in mind, let's write some code!
class QueueTwoStacks(object):
def __init__(self):
self.in_stack = []
self.out_stack = []
def enqueue(self, item):
self.in_stack.append(item)
def dequeue(self):
if len(self.out_stack) == 0:
# Move items from in_stack to out_stack, reversing order
while len(self.in_stack) > 0:
newest_in_stack_item = self.in_stack.pop()
self.out_stack.append(newest_in_stack_item)
# If out_stack is still empty, raise an error
if len(self.out_stack) == 0:
raise IndexError("Can't dequeue from empty queue!")
return self.out_stack.pop()
Complexity
Each enqueue is clearly time, and so is each dequeue when out_stack has items. Dequeue on an empty out_stack is order of the number of items in in_stack at that moment, which can vary significantly.
Notice that the more expensive a dequeue on an empty out_stack is (that is, the more items we have to move from in_stack to out_stack), the more -time dequeues off of a non-empty out_stack it wins us in the future. Once items are moved from in_stack to out_stack they just sit there, ready to be dequeued in time. An item never moves "backwards" in our data structure.
We might guess that this "averages out" so that in a set of enqueues and dequeues the total cost of all dequeues is actually just . To check this rigorously, we can use the accounting method, counting the time cost per item instead of per enqueue or dequeue.
So let's look at the worst case for a single item, which is the case where it is enqueued and then later dequeued. In this case, the item enters in_stack (costing 1 push), then later moves to out_stack (costing 1 pop and 1 push), then later comes off out_stack to get returned (costing 1 pop).
Each of these 4 pushes and pops is time. So our total cost per item is . Our enqueue and dequeue operations put or fewer items into the system, giving a total runtime of .
What We Learned
People often struggle with the runtime analysis for this one. The trick is to think of the cost per item passing through our queue, rather than the cost per enqueue() and dequeue().
This trick generally comes in handy when you're looking at the time cost of not just one call, but "m" calls.
Parenthesis Matching
I like parentheticals (a lot).
"Sometimes (when I nest them (my parentheticals) too much (like this (and this))) they get confusing."
Write a function that, given a sentence like the one above, along with the position of an opening parenthesis, finds the corresponding closing parenthesis.
Example: if the example string above is input with the number 10 (position of the first parenthesis), the output should be 79 (position of the last parenthesis).
Hint 1
How would you solve this problem by hand with an example input?
Hint 2
Try looping through the string, keeping a count of how many open parentheses we have.
Hint 3
Solution
We simply walk through the string, starting at our input opening parenthesis position. As we iterate, we keep a count of how many additional "(" we find as open_nested_parens. When we find a ")" we decrement open_nested_parens. If we find a ")" and open_nested_parens is 0, we know that ")" closes our initial "(", so we return its position.
def get_closing_paren(sentence, opening_paren_index):
open_nested_parens = 0
for position in range(opening_paren_index + 1, len(sentence)):
char = sentence[position]
if char == '(':
open_nested_parens += 1
elif char == ')':
if open_nested_parens == 0:
return position
else:
open_nested_parens -= 1
raise Exception("No closing parenthesis :(")
Complexity
time, where is the number of chars in the string. space.
The for loop with range keeps our space cost at . It might be more Pythonic to use:
for char in sentence[position:]:
but then our space cost would be , because in the worst case position would be 0 and we'd take a slice of the entire input.
What We Learned
The trick to many "parsing" questions like this is using a stack to track which brackets/phrases/etc are "open" as you go.
So next time you get a parsing question, one of your first thoughts should be "use a stack!"
In this problem, we can realize our stack would only hold '(' characters. So instead of storing each of those characters in a stack, we can store the number of items our stack would be holding.
That gets us from space to space.
It's pretty cool when you can replace a whole data structure with a single integer.
Bracket Validator
You're working with an intern that keeps coming to you with JavaScript code that won't run because the braces, brackets, and parentheses are off. To save you both some time, you decide to write a braces/brackets/parentheses validator.
Let's say:
(,{,[are called openers.),},]are called closers.
Write an efficient function that tells us whether or not an input string's openers and closers are properly nested.
Examples:
"{ [ ] ( ) }"should returntrue"{ [ ( ] ) }"should returnfalse"{ [ }"should returnfalse
Hint 1
We can use a greedy approach to walk through our string character by character, making sure the string validates "so far" until we reach the end.
What do we do when we find an opener or closer?
Hint 2
Well, we'll need to keep track of our openers so that we can confirm they get closed properly. What data structure should we use to store them? When choosing a data structure, we should start by deciding on the properties we want. In this case, we should figure out how we will want to retrieve our openers from the data structure! So next we need to know: what will we do when we find a closer?
Hint 3
Suppose we're in the middle of walking through our string, and we find our first closer:
[ { ( ) ] . . . .
^
How do we know whether or not that closer in that position is valid?
Hint 4
A closer is valid if and only if it's the closer for the most recently seen, unclosed opener. In this case, ( was seen most recently, so we know our closing ) is valid.
So we want to store our openers in such a way that we can get the most recently added one quickly, and we can remove the most recently added one quickly (when it gets closed). Does this sound familiar?
Hint 5
What we need is a stack!
Hint 6 (solution)
Solution
We iterate through our string, making sure that:
- each closer corresponds to the most recently seen, unclosed opener
- every opener and closer is in a pair
We use a stack to keep track of the most recently seen, unclosed opener. And if the stack is ever empty when we come to a closer, we know that closer doesn't have an opener.
So as we iterate:
- If we see an opener, we push it onto the stack.
- If we see a closer, we check to see if it is the closer for the opener at the top of the stack. If it is, we pop from the stack. If it isn't, or if the stack is empty, we return
false.
If we finish iterating and our stack is empty, we know every opener was properly closed.
def is_valid(code):
openers_to_closers = {
'(' : ')',
'{' : '}',
'[' : ']',
}
openers = set(openers_to_closers.keys())
closers = set(openers_to_closers.values())
openers_stack = []
for char in code:
if char in openers:
openers_stack.append(char)
elif char in closers:
if not openers_stack:
return False
else:
last_unclosed_opener = openers_stack.pop()
# If this closer doesn't correspond to the most recently
# seen unclosed opener, short-circuit, returning False
if not openers_to_closers[last_unclosed_opener] == char:
return False
return openers_stack == []
Complexity
time (one iteration through the string), and space (in the worst case, all of our characters are openers, so we push them all onto the stack).
Bonus
In Ruby, sometimes expressions are surrounded by vertical bars, "|like this|". Extend your validator to validate vertical bars. Careful: there's no difference between the "opener" and "closer" in this case-—they're the same character!
What We Learned
The trick was to use a stack.
It might have been difficult to have that insight, because you might not use stacks that much.
Two common uses for stacks are:
- parsing (like in this problem)
- tree or graph traversal (like depth-first traversal)
So remember, if you're doing either of those things, try using a stack!